Пространственное распределение - нейтрон
Cтраница 1
Пространственное распределение нейтронов, обусловленное их диффузией в процессе замедления, определяет вероятность потери нейтронов для ядерного реактора и влияет на его критич. [1]
Описать пространственное распределение нейтронов всех энергий посредством единственной функции невозможно и, следовательно, вообще невозможны аналитические решения для таких систем. Единственный способ преодолеть эти трудности заключается во введении энергетических групп. При этом сплошную область замедления разбивают на энергетические интервалы, а для описания пространственного распределения нейтронов в каждой группе используют односкоростные диффузионные дифференциальные уравнения. Но так как различные группы связаны между собой плотностью замедления, это приближение часто приводит к громоздкой системе связанных друг с другом уравнений, которую лучше решать с помощью быстродействующих вычислительных машин. [2]
Для анализа пространственного распределения нейтронов в активной зоне широко пользуются односкоростной теорией. [3]
Ограниченная кривой пространственного распределения нейтронов площадь А, которую определяют обычно графическим. Мы рассматриваем только тепловые-нейтроны. Измерение площади может служить или ( если сохранять постоянной среду) для сравнения выходов различных источников, или ( если сохранять постоянным источник) для измерения среднего сечения поглощения среды. [4]
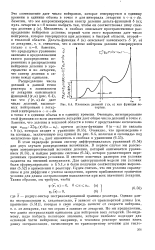 |
Плотность делений / ( г, и как функция летаргии. [5] |
Множитель в скобках описывает пространственное распределение нейтронов деления; первый член этого выражения дает число нейтронов, которое генерируется при делениях в быстрой области, второй - в тепловой области. Заметим, что предыдущее уравнение записано в предположении такого распределения переменных в распределении нейтронов деления в пространстве и по летаргии, что спектр деления в системе всюду одинаков. [6]
Применим уравнения диффузии для определения пространственного распределения нейтронов в бесконечной среде, содержащей элементарные источники нейтронов различной геометрии. Результаты, полученные в этих расчетах, применим к диффузионным задачам с более сложным распределением источников и к системам конечных размеров. [7]
Обсудим теперь важную проблему о пространственном распределении нейтронов. [8]
Уравнение ( 8.256 6) дает пространственное распределение нейтронов всех энергий по всему объему реактора. Решениями этого уравнения является совокупность собственных функций i n ( r), соответствующих собственным значениям Кп [ ср. [9]
Замедляющая и поглощающая способности горных пород определяют пространственное распределение нейтронов в исследуемой среде по энергиям в последовательно разные времена их жизни. [10]
Вследствие того, что наличие стержня приводит к нарушению всего пространственного распределения нейтронов в котле, существенным является не только появление утечки нейтронов, обусловленной непосредственно самим стержнем, но и изменение утечки нейтронов из котла наружу. В рассмотрении, в котором все сводится к некоторым изменениям геометрии котла, учитываются одновременно оба эти явления. [11]
Определенный в предыдущем параграфе квадрат длины замедления нейтронов является важной характеристикой пространственного распределения нейтронов. Нахождение точного вида функции распределения представляет собой чрезвычайно сложную задачу, решение которой известно только в некоторых частных случаях. Мы говорили выше, что знание всех моментов функции распределения ( квадрат длины замедления пропорционален второму моменту) дает в принципе возможность определить функцию распределения, но последовательное нахождение моментов приводит к громоздким и необозримым формулам, так что этот метод нахождения функции распределения является мало эффективным. Однако во многих случаях при определении функции распределения достаточно пользоваться приближенным методом, основанным на замене точного интегро-дифференциального кинетического уравнения дифференциальным уравнением. Это уравнение является уравнением диффузионного типа и поэтому само приближение называется диффузионным. Диффузионное приближение является законным, как мы увидим далее, в области энергий, малых по сравнению с начальной энергией нейтронов, и на расстояниях от источника, малых по сравнению с r2 / / s; кроме того, длина свободного пробега должна быть достаточно медленно-меняющейся функцией энергии. [12]
Определенный в предыдущем параграфе квадрат длины замедления нейтронов является важной характеристикой пространственного распределения нейтронов. Нахождение точного вида функции распределения представляет собой чрезвычайно сложную задачу, решение которой известно только в некоторых частных случаях. Мы говорили выше, что знание всех моментов функции распределения ( квадрат длины замедления пропорционален второму моменту) дает в принципе возможность определить функцию распределения, но последовательное нахождение моментов приводит к громоздким и необозримым формулам, так что этот метод нахождения функции распределения является мало эффективным. Однако во многих случаях при определении функции распределения достаточно пользоваться приближенным методом, основанным на замене точного интегро-дифференциального кинетического уравнения дифференциальным уравнением. Это уравнение является уравнением диффузионного типа и поэтому само приближение называется диффузионным. Диффузионное приближение является законным, как мы увидим далее, в области энергий, малых по сравнению с начальной энергией нейтронов, и на расстояниях от источника, малых по сравнению с r2 / ls; кроме того, длина свободного пробега должна быть достаточно медленно-меняющейся функцией энергии. [13]
Расчет этих факторов в каждом случае сводится, как правило, к определению пространственного распределения нейтронов всех энергий. [14]
Конечно, число нейтронов во втором поколении, вообще говоря, зависит от пространственного распределения нейтронов первого поколения. Поэтому правильное значение коэффициента размножения для реактора получается в том случае, когда используют такое распределение источников, которое повторяет себя в следующем поколении. [15]
Страницы: 1 2 3