Пространственное распределение - нейтрон
Cтраница 3
Описать пространственное распределение нейтронов всех энергий посредством единственной функции невозможно и, следовательно, вообще невозможны аналитические решения для таких систем. Единственный способ преодолеть эти трудности заключается во введении энергетических групп. При этом сплошную область замедления разбивают на энергетические интервалы, а для описания пространственного распределения нейтронов в каждой группе используют односкоростные диффузионные дифференциальные уравнения. Но так как различные группы связаны между собой плотностью замедления, это приближение часто приводит к громоздкой системе связанных друг с другом уравнений, которую лучше решать с помощью быстродействующих вычислительных машин. [31]
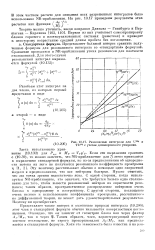 |
Резонансные интегралы для U238 Th232 с учетом допцлеровского уширения. [32] |
Эту величину рассчитывают обычно с помощью одно скоростной модели в предположении, что все нейтроны быстрые. Нужно отметить, что эта точка зрения недостаточно ясна. С одной стороны, когда используется NR-приближение, это означает, что требуется только одно столкновение для того, чтобы вывести резонансный нейтрон из окрестности резонанса; таким образом, пространственное распределение нейтронов очень близко к однородному и изотропному. С другой стороны, поглощение очень велико и использование коэффициента проигрыша, рассчитанного по диффузионной теории, не может дать удовлетворительных результатом. [33]
Это значит, что данное соотношение является соответствующим уравнением баланса нейтронов для мультиплицирующей среды в стационарном состоянии в односкоростном приближении ( ср. Наоборот, решения диффузионного уравнения будут точно также удовлетворять кинетическому уравнению в случае бесконечной среды. Решения диффузионного уравнения для конечной геометрии не удовлетворяют кинетическому уравнению, однако, если решение относится к областям, далеким от границы, оно будет приближенно удовлетворять кинетическому уравнению. В этих областях угловое распределение потока близко к изотропному, и результаты диффузионной теории могут давать хорошее приближение пространственного распределения нейтронов. [34]
В разделе 9 мы уже рассматривали замедление нейтронов, причем мы интересовались временем, которое проходит от момента появления нейтрона до того момента, когда нейтрон замедлится до верхней границы области энергий, в которой справедлив зако-н 1 / - у. В разделе 10 был рассмотрен процесс резонансного поглощения. Соображения, положенные в основу, и выводы обоих разделов остаются справедливыми, независимо от того, имеет ли место резонансное поглощение для тех нейтронов, которые остались бы внутри котла в отсутствие резонансного поглощения. Поскольку мы интересуемся либо расчетом критических размеров, либо законом развития процесса в котле во времени, постольку нас может не интересовать дальнейшая судьба нейтронов, вышедших из котла. Однако есть и другая, весьма важная сторона процесса замедления, которая нас интересует, когда мы рассматриваем рождение нейтронов при делении в котле. Прежде чем эти нейтроны станут тепловыми, они могут пройти большие расстояния, а пространственное распределение нейтронов в процессе их замедления играет основную роль при определении критических размеров. [35]
Страницы: 1 2 3