Нормальное распределение

Cтраница 1

Нормальное распределение не обладает тем свойством, что величина принимает только положительные значения, и легко видеть, что для такого распределения величина V неограничена, так что условие 2) не выполняется. [1]

Нормальное распределение часто называют еауссовским распределением f но оно использовалось в теории вероятностей еще Муавром и Лапласом. [2]

Нормальное распределение и распределение Коши свидетельствуют, что безгранично делимое распределение не обязано принадлежать обобщенному пуассоновскому типу. Однако мы покажем, что любое безгранично делимое распределение является пределом последовательности обобщенных пуассоновских распределений. [3]

Нормальное распределение ( в некоторых случаях - логарифмически нормальное) характерно для износовых отказов, имеющих место при длительной эксплуатации или длительных испытаниях элементов. [4]

Нормальное распределение является наиболее часто используемой моделью, его применяют в теории надежности для описания отказов, вызванных износом деталей. [5]

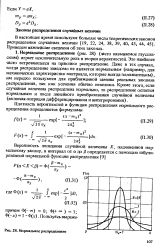Нормальное распределение. [6]

Нормальное распределение ( рис. 28) ( часто называемое гауссов-ским) играет исключительную роль в теории вероятностей. Это наиболее часто встречающееся на практике распределение. Даже в тех случаях, когда распределение заведомо не является нормальным ( например, для механических характеристик материала, которые всегда положительны), им нередко пользуются для приближенной замены реальных законов распределения, так как усечения обычно невелики. [7]

Нормальное распределение не следует применять для тех характеристик меха. [8]

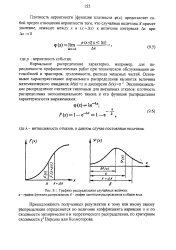Графики распределения случайных величин. а - график функций распределения. б - график плотности распределения в общем виде. [9]

Нормальное распределение характерно, например, для периодичности профилактических работ при техническом обслуживании автомобилей и тракторов, трудоемкости, расхода запасных частей. [10]

Нормальное распределение ( закон Гаусса) находит самое широкое практическое применение. Главная особенность, выделяющая нормальное распределение среди других законов, состоит в том, что оно является предельной формой многих распределений. [11]

Нормальное распределение встречается в тех случаях, когда случайная величина принимает значения, являющиеся результатом совместного действия многих независимых причин, хотя роль каждой причины в отдельности мала. Нормальный закон распределения широко применяется в измерительной технике и автоматике. [12]

Нормальное распределение характерно для непрерывных случайных величин, флуктуации которых относительно среднего равновероятны по знаку, невелики по сравнению с самой измеряемой величиной и являются результатом воздействия большого числа отдельных независимых факторов, вклады которых сравнимы по величине и аддитивны. Именно поэтому погрешности большинства прямых измерений подчиняются нормальному закону распределения. [13]

Плотность и функция распределения стандартной нормальной величины. [14]

Нормальное распределение - это наиболее часто встречающееся в статистике и в теории вероятностей распределение. [15]

Страницы: 1 2 3 4 5