Нормальное распределение

Cтраница 3

Построение распределения параметра х по данным ограниченного числа испытаний для определения р ( ж а с наибольшей надежностью. [31]

Нормальное распределение становится полностью известным, если заданы значения х р и а. Знаки плюс или минус в формулах принимают в зависимости от задач расчета. [32]

Нормальное распределение применяется исходя из гипотезы, что в каждом крупном отделе или цехе, по всей вероятности, имеются сотрудники как с хорошими, так и с менее хорошими показателями успешности труда. Если имеются существенные отклонения от нормального распределения, то итоги оценки дополнительно анализируются и возможно проведение дополнительной аттестации с привлечением большего числа оценивающих. [33]

Нормальное распределение является статистической моделью для суммы большого числа независимых ( или слабозависимых) величин, имеющих конечные средние и дисперсии, и с высокой точностью описывает ошибку измерения. Центральный член разложения некоторых распределений, отличных от нормального, хорошо аппроксимируется нормальной функцией. Для описания времени жизни применяют нормальное или усеченно нормальное распределение. [34]

Нормальное распределение е можно объяснить с помощью центральной предельной теоремы теории вероятностей, ибо на величину е оказывают влияние значительное количество случайных факторов, каждый из которых влияет незначительно. [35]

Нормальное распределение связано некоторым образом с процессом размазывания. Формализм независимых случайных величин, видимо, приводит к потере ощущения комбинаторной сути. Нечто подобное этому может служить причиной появления Jexp ( - x2) dx в большинстве примеров разд. [36]

Нормальное распределение является одним из наиболее важных распределений. Именно оно будет играть значительную роль в следующих главах. [37]

Нормальное распределение называют также гауссовским. [38]

Нормальное распределение имеет основополагающее значение для многих статистических оценок и тестов. Оно особенно удобно для описания таких случайных процессов высоковольтной техники, как пробой воздушных промежутков и пробой по поверхности изоляторов ( см. § 4.2), однако находит широкое применение и для описания процессов в других областях. В высоковольтной технике инженерные расчеты, связанные с многочисленными преобразованиями, основаны на нормальном распределении, ссылки на которые лучше всего говорят инженеру о необходимости всегда иметь его в своем распоряжении. [39]

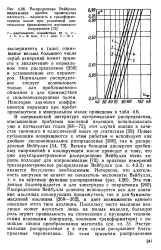Распределение Вейбулла напряжения пробоя промежутка плоскость - плоскость в трансформаторном масле при различной длительности приложенного переменного напряжения. [40]

Нормальное распределение следует использовать только для приближенного описания и для промежутков с сильнонеоднородным полем. [41]

Нормальное распределение - лишь частный и довольно редкий случай распределения экономических показателей или связанных с ними технико-технологических параметров. [42]

Нормальное распределение возникает тогда, когда отклонение случайной величины создают многие примерно равнозначные по воздействию независимые ( или слабо зависимые) между собой факторы, каждый из которых оказывает на случайную величину сравнительно малое влияние. [43]

Нормальное распределение имеет нулевой эксцесс, Независимость от времени математического ожидания и дисперсии характеризует стационарность сигнала, а отклонение его от нормальноети выявляют асимметрия и эксцесс, Все эти характеристики моп т 1шть использованы II качестве диагностических признаков. [44]

Нормальное распределение было открыто Муавром в 1733 г. и затем детально изучалось Лапласом и Гауссом. [45]

Страницы: 1 2 3 4 5