Нормальное распределение

Cтраница 2

Нормальное распределение широко используется в разнообразных физических и инженерных задачах, например для описания ошибок измерений. Вместе с тем следует особо отметить, что многие явления не могут быть описаны нормальным законом, например экстремальные скорости ветра, соответствующие любому заданному географическому району. [16]

Нормальные распределения широко используются, так как об ладают многими важными свойствами. Рассмотрим некоторые из них. [17]

Нормальные распределения широко используются, так как обладают многими важными свойствами. Рассмотрим некоторые из них. [19]

Нормальное распределение описывает поведение непрерывных величин, однако может применяться не ко всем из них. Например, вариация объемов выпуска продукции обычно подчиняется нормальному закону, равно как и спрос на продукт, но другие переменные, такие как вариация времени обслуживания заказа, могут иметь иное распределение. Вообще, если наблюдаемая величина более-менее симметрично распределяется относительно своего среднего значения, можно применять нормальный закон. Чаще всего он используется в контроле процессов, поскольку отклонения в работе оборудования практически всегда носят нормальный характер. [20]

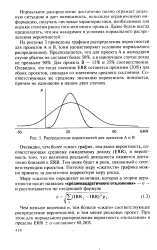Распределение вероятностей для проектов А и В. [21]

Нормальное распределение достаточно полно отражает реальную ситуацию и дает возможность, используя ограниченную информацию, получать числовые характеристики, необходимые для оценки степени риска того или иного проекта. [22]

Нормальное распределение выступает в качестве одного из наиболее используемых в вероятностных вычислениях. Одномерное нормальное распределение хорошо изучено; в MathCAD Pro имеются необходимые встроенные функции ( см. табл. 3.6) для его анализа. Некотороые из этих функций были применены в предыдущем разделе. [23]

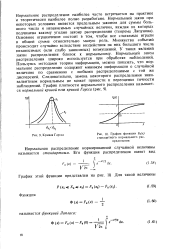Кривая Гаусса.| График функции Fa ( x стандартного нормального распределения. [24]

Нормальное распределение наиболее часто встречается на практике и теоретически наиболее полно разработано. Основное ограничение состоит в том, чтобы все слагаемые играли в общей сумме относительно малую роль. Множество событий происходит случайно вследствие воздействия на них большого числа независимых ( или слабо зависимых) возмущений. У таких явлений закон распределения близок к нормальному. Нормальный закон распределения широко используется при обработке наблюдений. Пользуясь методами теории информации, можно показать, что нормальное распределение содержит минимум информации о случайной величине по сравнению с любыми распределениями с той же дисперсией. Следовательно, замена некоторого распределения эквивалентным нормальным не может привести к переоценке точности наблюдений. [25]

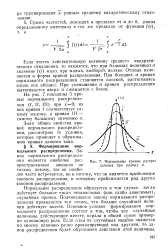Нормальные кривые распределения при разных 0. [26]

Нормальное распределение образуется в том случае, когда действует большое число независимых ( или слабо зависимых), случайных причин. Подчиненность закону нормального распределения проявляется тем точнее, чем больше случайных величин действует вместе. Основное условие формирования нормального распределения состоит в том, чтобы все случайные величины, действующие вместе, играли в общей сумме примерно одинаковую роль. Если одна из случайных ошибок окажется по своему влиянию резко превалирующей над другими, то закон распределения будет обусловлен действием этой величины. [27]

Квантили распределения Колмогорова. [28]

Нормальное распределение полностью определяется двумя параметрами - математическим ожиданием тх и стандартом ах. Все остальные моменты нормального распределения выражаются через математическое ожидание и стандарт. [29]

Нормальное распределение является лишь предельным, идеальным распределением. Однако при исследовании многих процессов, протекающих в вероятностных условиях, возникает вопрос о близости распределения результатов к нормальному. Оценка степени приближения основывается на свойствах нормального распределения. В качестве критерия оценки используют х2 ( хи-квадрат) - критерий, а также такие характеристики распределения, как эксцесс и коэффициент асимметрии. [30]

Страницы: 1 2 3 4 5