Гауссовское распределение

Cтраница 1

Гауссовское распределение огибающей корреляционной функции приводит к гауссовскому энергетическому спектру. [1]

Гауссовское распределение по термодинамическому потенциалу означает отличную от нуля вероятность образования высокомолекулярных веществ в процессе химического превращения низкомолекулярных компонентов. [2]

Гауссовские распределения обладают следующим экстремальным свойством. [3]

Гауссовское распределение (5.6.22) часто представляет собой приближение к истинному полю на плоскости z 0 на расстояниях р, не превышающих некоторого значения р - а. Если а значительно больше, чем WQ, то эффект использования приближения поля на плоскости z 0 полным гауссовским распределением является, как правило, пренебрежимо малым при определении поля во всем полупространстве z О, в котором распространяется луч. [4]

Гауссовские распределения часто называют нормальными. [5]

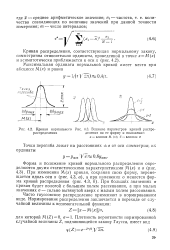Кривая нормального [ IMAGE ] Влияние параметров кривой распре-распределения деления на ее форму и положение. [6]

Часто гауссовское распределение применяют в нормированном виде. [7]

Для совместного гауссовского распределения линия регрессии допускает геометрическую интерпретацию. В этом важном случае коэффициенты регрессии суть тангенсы углов наклона главных осей эллипса постоянной вероятности. [8]

Формулы ВТИ. [9]

При гауссовском распределении между средней квадратической ошибкой регулирования и ее энтропией существует однозначная связь. Несмотря на математическую общность обоих критериев последний является более строгим, снимая, по сути дела, вопрос о вынужденной необходимости использования гауссовского распределения из-за незнания истинного. При гауссовском распределении энтропия ошибки регулирования максимальная, а действие помех наиболее эффективно. [10]

При гауссовском распределении и достаточно большом N оба критерия стремятся к нулю. [11]

При гауссовском распределении вынуждающей силы среднее число выбросов процесса q ( t) за уровень b на интервале времени ( О, Т) определяется следующим выражением. [12]

При гауссовском распределении вероятностей значений процесса X ( t) имеет место равенство ткгтк. [13]

Теоретическая форма плотности вероятности х Ret, соответствующая. а - полю одномодового лазера со случайной фазой [ ], б - излучению теплового источника [ ], в - суперпозиции двух полей одномодовых лазеров [ ] ( Mandel, 1965. [14]

Это есть гауссовское распределение комплексной переменной г, которое, как видно, тождественно по форме соответствующему распределению вероятности, возникающему при классическом описании теплового света. [15]

Страницы: 1 2 3 4