Биномиальное распределение

Cтраница 1

Биномиальное распределение нетрудно обобщить на случай последовательных независимых испытаний, каждое из которых заканчивается одним из нескольких возможных исходов. [1]

Биномиальное распределение является распределением дискретной случайной переменной, поскольку величины т могут принимать только вполне определенные целые значения. [2]

Биномиальное распределение используется для описания дискретных случайных величин. [3]

Биномиальное распределение имеет широкое распространение в практической деятельности людей. Например, продолжительное наблюдение за качеством выпускаемой заводом продукции показало, что р-я часть ее является браком. Иначе говоря, мы выражаем через р вероятность для любого изделия оказаться бракованным. [4]

Биномиальное распределение, возвращает значение вероятности Р ( х k), где n и k - целые числа, причем 0 k riHO pl k - случайная величина для биномиального распределения. [5]

Биномиальное распределение можно легко обобщить на случай п повторных независимых испытаний, каждое из которых может иметь несколько исходов. [6]

Биномиальное распределение имеет место, когда равновероятно появление отказа в любом из приводов при испытаниях случайной выборки. [7]

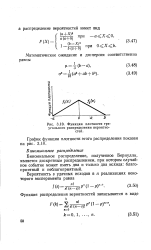Функция плотности треугольного распределения вероятностей. [8]

Биномиальное распределение, полученное Бернулли, является дискретным распределением, при котором случайное событие может иметь два и только два исхода: благоприятный и неблагоприятный. [9]

Биномиальное распределение и распределение Пуассона стремятся к нормальному, когда их математические ожидания стремятся к бесконечности. Эта особенность объясняется почти во всех книгах по теории вероятностей. [10]

Биномиальное распределение ( табл. 18.8 - 3), распределение Пуассона ( табл. 18.8 - 4) и распределение Коша ( табл. 18.8 - 8) устойчивы ( самовоспроизводятся) при сложении независимых величин. [11]

Биномиальное распределение дает вероятности X для каждого из результатов. [12]

Биномиальное распределение широко, используется в теории и практике статистического контроля качества продукции, при описании функционирования систем массового обслуживания, в теории стрельбы и в других областях практической деятельности. [13]

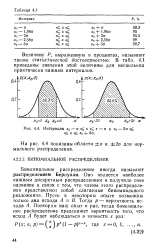Интервалы х0 - а дг дг-а и ха - 2а х g x0 2а. [14]

Биномиальное распределение иногда называют распределением Бернулли. Оно является наиболее важным дискретным распределением и получило свое название в связи с тем, что члены этого распределения представляют собой слагаемые биномиального разложения. Пусть в некотором опыте возможны только два исхода А и В. [15]

Страницы: 1 2 3 4