Биномиальное распределение

Cтраница 2

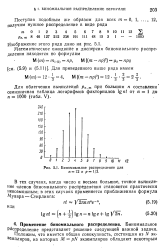Биномиальное распределение для и - 12 и р 1 / 3. [16]

Биномиальное Распределение представляет решение следующей важной задачи. [17]

Биномиальное распределение является важнейшим дискретным распределением, то есть распределением, которое сосредоточено всего лишь в нескольких точках. Этим точкам биномиальное распределение приписывает ненулевые вероятности. Таким образом, биномиальное распределение отличается от всех разобранных выше распределений ( нормального, хи-квадрат и др.), которые приписывают нулевые вероятности отдельно выбранным точкам и называются непрерывными. [18]

Биномиальное распределение ( 1) случайной величины ц имеет Мц р и Оц / гр7 ( см. задачу 3 вгл. Обозначим а Jnpq среднее квадратическое отклонение. [19]

Биномиальное распределение ( распределение Бернулли) описывает дискретные события следующего типа. И пусть условия таковы, что в каждом из экспериментов событие либо наблюдается, либо нет. Если вероятность обнаружения в отдельном опыте равна Р ( А) р, то в серии из п экспериментов следовало бы ожидать пр событий. [20]

Биномиальное распределение довольно широко используется в статистике, различных вероятностных расчетах. [21]

Биномиальное распределение ( табл. 18.8 - 3), распределений, Пуассона ( табл. 18.8 - 4) и распределение Коши ( табл. 18.8 - 8) устойчивы ( самовоспро изводятся) при сложении независимых величин. [22]

Биномиальное распределение является дискретным; его-нельзя рассматривать как непрерывную функцию времени. Оно применяется обычно в случаях, когда изделия классифицируются на хорошие и дефектные. Это распределение можно также применять при рассмотрении кратковременных операций, когда учет времени не имеет значения, например в пиротехнике. [23]

Биномиальное распределение -, пример неравномерного распределения дискретной конечно-значной случайной величины. [25]

Биномиальное распределение играет большую роль в элементарной теории вероятностей. Оно используется при решении многих задач. [26]

Биномиальное распределение имеет два свойства: 1) при вероятности р f 0 5 полигон распределения несимметричен ( фиг. [27]

Биномиальное распределение имеет место в следующих условиях. [28]

Биномиальное распределение, или распределение Бернулли, встречается в задачах о вычислении числа появления событий при повторении п независимых, испытаний с неизменной вероятностью р в каждом отдельном испытании ( см. также пп. Оно находит применение при контроле качества продукции и в других задачах. [29]

Биномиальное распределение является дискретным; его-нельзя рассматривать как непрерывную функцию времени. Оно-применяется обычно в случаях, когда изделия классифицируются на хорошие и дефектные. Это распределение можно также применять при рассмотрении кратковременных операций, когда, учет времени не имеет значения, например в пиротехнике. [30]

Страницы: 1 2 3 4