Экспоненциальное распределение

Cтраница 1

Экспоненциальное распределение является частным случаем и гамма-распределения, и распределения Вейбулла. [1]

Экспоненциальное распределение имеет место в случаях, когда аппаратура сложна и возможно большое число отказов различных элементов аппаратуры с разной интенсивностью. [2]

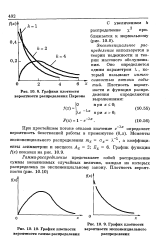Графики плотности вероятности распределения Пирсона.| График плотности вероятности гамма-распределения.| График плотности. [3]

Экспоненциальное распределение используется в теории надежности и теории массового обслуживания. Оно определяется одним параметром X, который называют интенсивностью потока событий. [4]

Экспоненциальное распределение в массовой форме использовалось в работах Пэймена. [5]

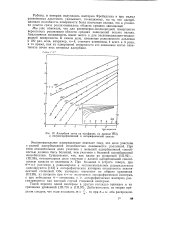Адсорбция азота на вольфраме, . ло данным 1341 ], ъ полулогарифмической и логарифмической шкалах. [6]

Экспоненциальное распределение отвечает тому, что доля участков с разной адсорбционной способностью оказывается различной. При этом относительная доля участков с меньшей адсорбционной способ-ностью должна быть большей, чем участков с большой адсорбционной способностью. При больших п ( строго говоря, при п - Voo) различия в равномерном и экспоненциальном распределениях нивелируются [133] и логарифмическая изотерма оказывается эквивалентной степенной. [7]

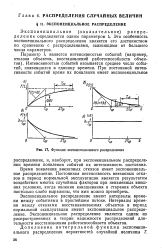Функции экспоненциального распределения. [8]

Экспоненциальное распределение имеют интервалы времени между событиями в простейшем потоке. Экспоненциальное распределение является одним из распространенных в теории надежности распределений длительности восстановления работоспособности объектов. [9]

Экспоненциальное распределение хорошо подходит в качестве модели отказов для УВС на базе ЭВМ, состоящей из большого числа элементов, отказ каждого из которых приводит к полному ее отказу. Для децентрализованных систем или систем с избыточностью эта модель отказов непригодна, так как отказы отдельных элементов и даже частей системы могут не сопровождаться ее полным отказом. [10]

Экспоненциальное распределение широко применяется в теориях надежности и массового обслуживания. [11]

Экспоненциальное распределение является распределением Пирсона X типа. [12]

Экспоненциальное распределение является одним из наиболее распространенных при исследовании надежности автоматизированных систем управления. Постоянство интенсивности отказов означает, что вероятность отказа не зависит от того, сколько времени проработало устройство до рассматриваемого момента времени. Это характерно для периода нормальной работы системы, так как при правильно организованной эксплуатации и профилактике АСУ ТП потоки отказов элементов близки к простейшим. Если система подошла к периоду износа или старения - закон распределения времени безотказной работы близок к нормальному. [13]

Кривая интенсивности отказов асинхронных двигателей. [14]

Экспоненциальное распределение имеет место только при постоянстве интенсивности внезапных отказов. Нормальное распределение ( двухпараметри-ческое) имеет место в том случае, когда на исследуемый объект воздействует целый ряд случайных факторов. [15]

Страницы: 1 2 3 4