Геометрическое распределение

Cтраница 1

Геометрическое распределение обладает важным свойством: у него нет последействия. [1]

Геометрическое распределение является единственным определенным на целых числах распределением вероятностей, для которого это утверждение верно, См. [2]

Геометрическое распределение имеет случайная величина, равная числу испытаний до первого успеха. [3]

Полученное геометрическое распределение интервалов на дискретном времени имеет место и для интервалов между заявками. [4]

Геометрическое распределение времени ожидания обладает интересным и важным свойством, которое отсутствует у всех остальных распределений. [5]

Геометрическое распределение времени ожидания обладает интересным и важным свойством, отличающим его от других распределений. Пусть нам известно, что в первых т испытаниях успехов не было; время ожидания T ( ffl) от т - неудачи до первого успеха имеет то же самое распределение qk и не зависит от числа предшествовавших неудач. [6]

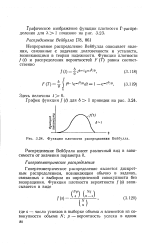Функция плотности распределения Вейбулла. [7]

Гипер геометрическое распределение является дискретным распределением, возникающим обычно в задачах, связанных с выбором из определенной совокупности без возвращения. [8]

Изучение геометрического распределения всех винтов, вдоль которых может перемещаться тело, обладающее свободой n - й степени, сводится, следовательно, к изучению распределения всех винтов, входящих в я-членную группу. В частности, винты, вдоль которых может совершать движение тело, имеющее три степени свободы, распределяются по гиперболоидам таким образом, что на каждом из гиперболоидов лежат винты одного и того же параметра; среди них есть гиперболоид нулевого параметра, отвечающий чистым вращательным движениям тела. [9]

Пусть имеет геометрическое распределение. [10]

На практике геометрическое распределение времени безотказной работы встречается довольно часто. Оно оказывается характерным для поломок инструментов на автоматических линиях, для отказов различных устройств автоматических линий при засорениях частицами стружки и в ряде других случаев. Поэтому полезен тщательный анализ физической природы этого распределения. В основу вывода, проделанного нами при решении задачи J3, положены в качестве главных два предположения. Первое: вероятность fo повреждения рабочего органа не зависит от номера изготавливаемого изделия или, иначе говоря, от того, сколько времени работал данный рабочий орган. [11]

Любая смесь геометрических распределений безгранично делима. [12]

Некоторые такого рода геометрические распределения являются теоретически обоснованными в отдельных частных задачах, и применение их в этих случаях вполне оправдано. Если такого рода схематизированные распределения служат, например, только для установления по ним временно принимаемых значений сравнительно грубых расчетных коэффициентов, зависящих главным образом от двух первых моментов распределения ( например, значений коэффициентов а и k при расчетах допусков составляющих звеньев размерных и кинематических цепей), то использование их еще можно считать в какой-то мере допустимым. [13]

Доказать, что геометрическое распределение безгранично делимо. [14]

В § 2.2 геометрическое распределение ( 2.2 - 2) толковалось как распределение вероятностей числа X бросаний кольца до первого попадания в цель. [15]

Страницы: 1 2 3 4