Каноническое распределение

Cтраница 1

Каноническое распределение широко применяется при решении частных задач статистической термодинамики. [1]

Каноническое распределение описывает систему, заключенную в жесткую, непроницаемую для частиц, но проводящую теплоту оболочку, так что система обменивается с окружением энергией. Nk, а энергия может изменяться. [2]

Каноническое распределение для квантовой системы принимает во внимание дискретность состояний. [3]

Каноническое распределение справедливо для любых независимых подсистем полной системы. В этой связи нужно особо отметить, что каноническое распределение не всегда можно применять к частицам идеального газа. [4]

Каноническое распределение может быть выведено из микроканонического. [5]

Каноническое распределение (7.20) определяет вероятность того, что координаты и проекции импульса имеют заданные значения. [6]

Здесь каноническое распределение (1.4.7) будет выведено методом, отличным от приведенного в разделе 1.4. Использование этого метода ( часто называемого методом Дарвина - Фаулера [205]) позволяет не только получить формулу (1.4.7) на основании общих принципов статистики ( в частности, эргодической гипотезы), но и интерпретировать распределение (1.4.7) как наиболее вероятное из всех возможных распределений вероятностей. [7]

Вывести каноническое распределение, считая, что термостатом являются: а) газ невзаимодействующих классических гармонических осцилляторов; б) газ невзаимодействующих ультрарелятивистских частиц е ср. [8]

В каноническое распределение явным образом входит температура. Благодаря этому легко устанавливается связь между статистическим и термодинамическим описанием одного и того же объекта. Это обуславливает его широкое применение в задачах статистической физики. [9]

Рассматривая каноническое распределение, мы всегда будем предполагать, что кратный интеграл в ( 92) имеет конечную величину, так как в противном случае коэффициент вероятности исчезает и закон распределения становится иллюзорным. Это исключает некоторые случаи, однако, очевидно, не такие, чтобы это повлияло на значение наших результатов; с точки зрения применения их к термодинамике. [10]

Применим квантовое каноническое распределение к вычислению средней энергии квантового гармонического осциллятора. [11]

Следовательно, каноническое распределение (1.4.7) в известном смысле можно трактовать как наиболее вероятное из всех возможных распределений вероятностей. В связи с этим процесс движения макросистемы к состоянию равновесия представляет собой по существу переход макросистемы из менее в более вероятное состояние. [12]

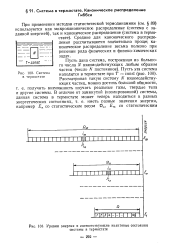Уровни энергии и соответствующие квантовые состояния системы в термостате. [13]

Средние для канонического распределения рассчитываются значительно проще; каноническое распределение весьма полезно при решении ряда физических и физико-химических задач. [14]

В случае канонических распределений мы избегаем такого положении. Очевидно, следовало бы провести доказательство равносильности, а это обычно делается поверхностно. Иногда эти распределения не являются равносильными, но я не буду здесь вас беспокоить этим. В простых случаях очевидно, что если число элементов подвергается не слишком большому изменению, то и результаты не будут черезчур различаться. [15]

Страницы: 1 2 3 4