Каноническое распределение - гиббс
Cтраница 3
СТАТИСТИЧЕСКАЯ СУММА - величина, обратная нормирующему множителю канонического распределения Гиббса в квантовой статистич. [31]
Мы опять нашли, что 0 есть модуль канонического распределения Гиббса. [32]
Речь идет о конструкции, известной физикам под названием канонического распределения Гиббса, а статистикам - под названием распределения экспоненциального типа. [33]
Системы, находящиеся в равновесии с термостатом, подчиняются каноническому распределению Гиббса. Температура, число частиц и внешние параметры таких систем считаются фиксированными, энергия и некоторые другие характеристики флуктуируют около равновесных значений. Согласно (25.1) расчет флуктуации потребует нахождения средних по распределению Гиббса. [34]
Эргодическое распределение состояний часто называется также микроканоническим в отличие от канонического распределения Гиббса, при котором функция распределения непрерывна и экспоненциально зависит от полной энергии. [35]
В заключение следует обратить внимание на аналогию между е-теоремой Больцмана и каноническим распределением Гиббса. [36]
Определим теперь распределение по состояниям открытой системы в термостате, называемое большим каноническим распределением Гиббса. [37]
Выражения ( 895) и ( 902) являются различными формами записи квантового канонического распределения Гиббса, которое характеризует распределение вероятностей различных состояний подсистем, находящихся в статистическом равновесии. [38]
Следовательно, переход к термодинамическому пределу для указанной системы оказывается невозможным, если допустить, что для нее верно каноническое распределение Гиббса; и, наоборот, предположение о существовании I lim LIN приводит к невозможности осуществления равновесного состояния с распределением Гиббса. [39]
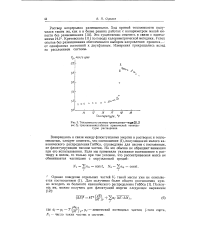 |
Теплоемкость системы триэтиламин-вода ( 21 2 вес. % триэтиламина вблизи критической температуры растворения. [40] |
Возвращаясь к связи между флюктуациями энергии в растворах и теплоемкостью, следует отметить, что соотношение ( 1), пол ученное из малого канонического распределения Гиббса, справедливо для систем с постоянным, не флюктуирующим числом частиц. На это обычно не обращают внимания при его использовании. [41]
Мы употребляем здесь и в следующем параграфе в качестве аргументов функции распределения величины q, р, t, так как при изложении приходится переходить к рассмотрению равновесного состояния и использовать каноническое распределение Гиббса. [42]
С другой стороны, при получении (1.123) имелись лишь два предположения: а) / lira ( L / N); L, N - - оо; б) плотность вероятности о задается каноническим распределением Гиббса. [43]
Поэтому произведение этих двух функций имеет очень резкий максимум при некотором значении энергии Е Е вер. Поэтому каноническое распределение Гиббса фактически эквивалентно микроканоническому распределению. [44]
Распределения (18.12) и (18.13) относятся к телу, находящемуся в равновесии с термостатом, иначе, являющемуся сравнительно малой частью некоторой большой замкнутой равновесной системы. Они называются каноническим распределением Гиббса и большим каноническим распределением Гиббса. Характеризуемые ими равновесные ансамбли называются соответственно каноническим и большим каноническим. [45]
Страницы: 1 2 3 4