Апостериорное распределение

Cтраница 1

Апостериорное распределение зависит от прошлого посредством функции G и ее аргументов, от текущего состояния, текущего вектора управления и преобразованного состояния. [1]

Апостериорное распределение ( 3) обладает некоторыми интересными свойствами. [2]

Хп апостериорное распределение W нормальное со средним ( t [ i nrX) / ( r - - пг) и мерой точности т пг. [3]

Рассмотрим теперь апостериорное распределение для R. [4]

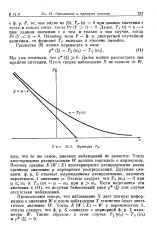Функция TF. [5]

Тогда апостериорное распределение W должно совпадать с априорным. Поэтому среднее Е ( W X) апостериорного распределения равно среднему значению ц априорного распределения. Если подставить эти значения в ( 11), то получим байесовский риск р () для случая отсутствия наблюдений. [6]

Но при указанном апостериорном распределении W вероятность того, что W лежит в интервале ( 8), равна у. Поэтому, согласно обычной теории, доверительный коэффициент этого интервала равен у, а согласно байесовской или субъективистской теории, вероятность попадания в этот интервал равна у. Поскольку оперативная интерпретация этих двух свойств по существу одна и та же, то, как уже отмечалось, выводы о W, основывающиеся на указанных двух точках зрения, вообще говоря, совпадают. [7]

Следовательно, эти апостериорные распределения, как и априорные, полностью характеризуются своими первыми моментами. Поэтому для каждого нового наблюдения нет необходимости пересчитывать всю плотность апостериорного наблюдения, а достаточно определять только два ее момента. [8]

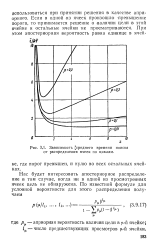Зависимость [ среднего времени поиска от распределения ячеек по циклам. [9]

Нас будет интересовать апостериорное распределение в том случае, когда ни в одной из просмотренных ячеек цель не обнаружена. [10]

Хп) обозначает апостериорное распределение W в конце n - го шага. Хп, но значения этих величин еще не известны, то апостериорное распределение следует рассматривать как случайное распределение. [11]

Сравнение формы апостериорного распределения сообщения с априорным. [12]

Приемник, вычисляющий апостериорное распределение вероятности pv ( x) и определяющий по заданному критерию передаваемое сообщение, называется оптимальным. Помехоустойчивость такого приемника является предельно достижимой. Такие приемники называются квазиоптимальными. [13]

Покажите, что апостериорное распределение параметра W на каждом шаге процедуры равномерное. [14]

Вид меры точности апостериорного распределения W особенно прост. [15]

Страницы: 1 2 3 4