Кривое распределение

Cтраница 1

Кривые распределения по уравнению Петрова. [1]

Кривые распределения микро - и переходных пор по размерам показали наличие максимума при 2 - 4 нм, который с повышением температуры обработки сдвигается в сторону больших радиусов. Форма петель гистерезиса при адсорбции-десорбции азота на коксах позволяет сделать заключение, что форма пор близка к цилиндрической. Реальное присутствие микропор и переходных пор, имеющих вид каналов, подтверждается электронно-микроскопическими исследованиями. [2]

Кривые распределения, построенные на основании данных наблюдений, получаются в виде ломаных линий не вполне правильной формы; их форма в большой степени зависит также от числа интервалов, на которые было разбито поле рассеивания при их построении. Вывод каких-либо закономерностей, имеющих общее значение, на основании рассмотрения таких кривых представляется затруднительным. [3]

Кривые распределения могут строиться по опытным данным или в некоторых случаях чисто умозрительно по теоретическим законам, отвечающим существенным признакам данной статистической совокупности. Имеются признаки ( Пирсона, Колмогорова, Бернштейна), по которым можно установить, что теоретическая кривая достаточно хорошо отвечает эмпирической. [4]

Кривые распределения получают путем преобразования столбчатых диаграмм. Для этого необходимо увеличение числа фракций и сужение интервалов каждой фракции. [5]

Кривые распределения интенсив - чаем то же условие (5.65), что и при ности в проходящем свете двухлучевой интерференции. [7]

Кривые распределения с положительной крутостью - эксцес-сивные кривые распределения - часто встречаются при обработке результатов химических измерений благодаря имеющимся при таких измерениях случайным большим ошибкам. [8]

Кривые распределения описываются непрерывными или дискретными дифференциальными и интегральными числовыми и массовыми функциями. Ими оперируют исключительно при кинетических расчетах. [9]

Кривые распределения в одной и той же области молекулярных весов могут характеризоваться различными значениями среднечис-лового молекулярного веса. При этом форма кривых распределения может быть весьма разнообразной с одним, двумя или несколькими максимумами. Соответствующие кривые называют уни -, би - и муль-тимодальными. Нетрудно представить себе кривые распределения с одинаковым Мп, но различной формы. Следовательно, среднечисловой молекулярный вес не является однозначной характеристикой кривой распределения. Зная величину Мп образца полимера, нельзя воспроизвести кривую распределения или хотя бы сделать вывод о числе максимумов на этой кривой. И все же Мп дает полезную информацию о свойствах полимеров и часто используется в кинетических расчетах. [10]

Кривые распределения описываются непрерывными или дискретными дифференциальными и интегральными числовыми и весовыми функциями. Ими оперируют исключительно при кинетических расчетах. Особый случай представляет собой описание МВР олигомеров, когда малый набор молекулярных весов резко изменяет картину при переходе от одной фракции к другой и распределение нельзя выразить непрерывной функцией. [11]

Кривые распределения стремятся к нулю при увеличении абсолютных значений погрешностей. [12]

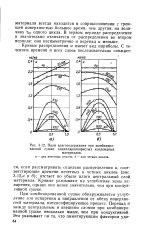Поля влагосодержания при комбинированной сушке капиллярнопористых коллоидных. [13]

Кривые распределения и имеют вид параболы. [14]

Кривые распределения симметричны и более островершинны, чем кривые закона Гаусса. [15]

Страницы: 1 2 3 4 5