Кривое распределение

Cтраница 3

Дифференциальные кривые распределения полиэфиров по молекулярным массам. [31]

Кривые распределения по молекулярной массе, вычисленные по уравнению Флори, при различной степени завершенности Р реакции поликондексации. [32]

Кривые распределения могут строиться по опытным данным или в некоторых случаях чисто умозрительно по теоретическим законам, отвечающим существенным признакам данной статистической совокупности. По признакам Пирсона, Колмогорова, Бернштейна можно установить, что теоретическая кривая достаточно хорошо отвечает эмпирической. [33]

Кривые распределения по формуле (4.43) при небольших значениях п ( до 10) изменяются по сравнению с исходной гауссовой кривой ( при той же системе координат и единицах отсчета 00 и 1 / 0 о) следующим образом: среднее значение и модальная ордината смещаются вправо ( доходят примерно до абсцисс, равных 1 5а), кривые становятся более островершинными, доходя в точке максимума до 0 71 / 00, и несколько асимметричными. [34]

Кривые распределения могут быть симметричными ( фиг. [35]

Кривые распределения определяются опытным путем методом седиментации. Дисперсность твердой фазы, ее порозность и форма частиц наряду с разностью плотностей обеих фаз и вязкостью жидкой среды являются важнейшими параметрами суспензий, определяющими выбор типа осадительной центрифуги и ее рабочего режима. [36]

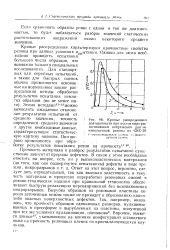Кривые распределения долговечности при постоянном растягивающем напряжении для ненаполненной резины из СКС-30. I-высокомодульная резина. 2-аизкомо-дульная резина. [37]

Кривые распределения характеризуют прочностные свойства резины при данных условиях испытания. [38]

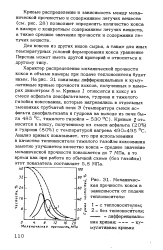Механическая прочность кокса в зависимости от подачи теплоносителя. [39]

Кривые распределения и зависимость между механической прочностью и содержанием летучих веществ ( см. рис. 28) позволяют определить количество кокса в камере с конкретным содержанием летучих веществ, а также средние значения прочности и содержания летучих веществ. [40]

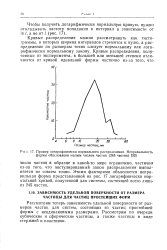Пример логарифмически нормального распределения. Неправильность формы обусловлена малым числом частиц ( 245 частиц. [41]

Кривые распределения можно рассматривать как гистограммы, в которых ширина интервалов стремится к нулю, а распределение по размерам точно следует нормальному или логарифмически нормальному закону. [42]

График плотности распределения равномерно распределенной случайной величины.| Кривые распределения Вейбулла. [43]

Кривые распределения для этого закона изображены на рис. 1.28. При а 1 закон распределения Вейбулла совпадает с показательным распределением, при а 1 интенсивность отказов является монотонно убывающей функцией, а при а 1 - монотонно возрастающей. Это обстоятельство дает возможность подбирать для опытных данных соответствующие значения параметров Х0 и а с тем, чтобы уравнение функции распределения наилучшим образом совпадало с опытными данными. [44]

Страницы: 1 2 3 4 5