Зарядовое распределение

Cтраница 1

Получено зарядовое распределение, используемое для решения разнообразного круга задач. [1]

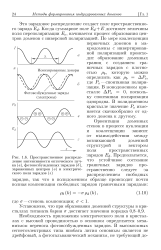Пространственное распределение интенсивности оптического пучка ( а, фотовозбужденных зарядов ( 5, заряженных центров ( в и электрического поля зарядов ( г. [2]

Это зарядовое распределение создает поле пространственного заряда ЕЛ. Когда суммарное поле Ed E достигает величины поля переполяризации Ес, начинается процесс образования центров доменов с инверсной поляризацией. [3]

Монополи я-электронных переходов в молекуле бутадиена, рассчитанные в металлической модели. Расстояния между центрами монополей даны в А, заряды монополей - в ат, ед. [4]

Эти зарядовые распределения в одних областях пространства положительны, в других отрицательны. [5]

В полное зарядовое распределение дают вклад положительные заряды ядер Za, которые всегда локализованы. [6]

Функция зарядового распределения равна нулю во всех случаях, кроме i ( H) t ( H), где V и i относятся к связывающей или разрыхляющей МО связи СН. [7]

Точный расчет зарядового распределения в ФРК при неоднородном освещении требует решения системы уравнений (4.5) - (4.7) для трехмерного случая, что является крайне сложной задачей. [8]

Для характеристики пофрагментных зарядовых распределений важны следующие величины: связывающий радиус - расстояние между ядром и межъядерной стационарной точкой [ для которой Vp ( r) OJ; несвязывающий радиус - расстояние по оси связи между ядром и контуром ( поверхностью), соответствующим некоторому значению электронной плотности, обычно 0 002 а. В двухатомных молекулах плоскость, проходящая через одно из ядер перпендикулярно к оси связи, разделяет зарядовую плотность фрагмента на связывающий и несвязывающий вклады; в многоатомных системах указанные области и направления связей определяются соответствующими градиентными траекториями, берущими начало в стационарной точке и оканчивающимися на ядрах. [9]

Линнет [44] исследовал относительные зарядовые распределения, отыскивая максимум квадрата детерминантных волновых функций в зависимости от изменений относительных положений всех электронов. [10]

Вследствие локализованного характера зарядового распределения роль обменных эффектов в межмо л окулярных взаимодействиях уменьшается по. [11]

Рассмотрение взаимодействий локализованных зарядовых распределений во втором порядке теории возмущений позволяет найти индукционное и дисперсионное взаимодействия. В работах Амоса и Криспина [ ИЗ, 114 ] были получены выражения длят этих взаимодействий через поляризуемость и диполы-ше моменты локальных зарядовых распределений. [12]

Обсудим некоторые вопросы зарядового распределения продуктов ядерного распада, поскольку от принципиальной возможности зарядового расщепления ( в результате многочисленных ядерных реакций) в осколках деления, обладающих наибольшей кинетической энергией, зависит в конечном итоге и решение задачи генерации лавинообразно возрастающей электрической энергии во внешней обмотке ядерного реактора нового типа - ядерного генератора. [13]

Несущественное преимущество приближенной замены зарядового распределения гауссовским состоит в том, что оно позволяет оценить все трехцентровые интегралы, не проводя разложения по мульти-полям. Следовательно, сразу же отпадают трудности, связанные с асимптотическим разложением. [14]

Существенное преимущество приближенной замены зарядового распределения гауссовским состоит в том, что оно позволяет оценить все трехцентровые интегралы, не проводя разложения по мульти-полям. Следовательно, сразу же отпадают трудности, связанные с асимптотическим разложением. [15]

Страницы: 1 2 3 4 5