Рассеивание - случайная величина
Cтраница 2
Дисперсия служит для показания степени рассеивания случайной величины относительно ее среднеожидаемого значения. [16]
На практике за границы зоны рассеивания случайной величины X принимают значения 0 и 3 44к, где к - параметр распределения. [17]
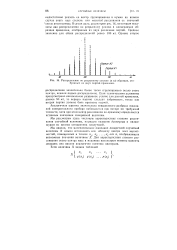 |
Распределение по разрывному усилию ( в кг образцов, отобранных из двух партий проволоки. [18] |
Мы рассмотрим здесь числовую характеристику степени рассеивания случайной величины, носящую название дисперсии и являющуюся во многих отношениях наилучшей. [19]
Характеристики ( некоторые параметры) расположения и рассеивания случайных величин позволяют численно выразить существенные особенности распределений случайных величин. [20]
Очевидно, что дисперсия уменьшается с уменьшением рассеивания случайной величины: чем уже участок, на котором сосредоточены значения случайной величины, тем меньше ее дисперсия. Поэтому на практике пользоваться дисперсией не совсем удобно. [21]
Одна из основных числовых характеристик совокупности, характеризующая степень рассеивания случайной величины, равная корню квадратному из дисперсии о [ х ] VAA: j ( близк. [22]
Чтобы представить смысл понятия дисперсии и среднеквадратичного отклонения как характеристики рассеивания случайной величины, рассмотрим примеры. [23]
Средний арифметический размер / определяет положение центра группирования или центра рассеивания случайных величин. [24]
Средний арифметический размер 7 определяет положение центра группирования или центра рассеивания случайных величин. [25]
Чтобы представить смысл понятия дисперсии и среднеквадратичного отклонения как характеристики рассеивания случайной величины, рассмотрим примеры. [26]
В силу этого в технике считают, что практическая зона рассеивания случайной величины X, следующей нормальному закону, равна бет. [27]
При малом числе наблюдений ( 10 - 15 и меньше) рассеивание случайных величин целесообразно характеризовать не а, а диапазоном рассеивания R. Остаточной погрешностью называется разность между размером, полученным в результате измерения, и средним арифметическим размером, который принимается за наиболее вероятный размер детали. [28]
Чтобы представить смысл понятия дисперсии и среднего крадра-тического отклонения как характеристики рассеивания случайной величины, рассмотрим примеры. [29]
Чтобы представить смысл понятия дисперсии и среднего квадра-тического отклонения как характеристики рассеивания случайной величины, рассмотрим примеры. [30]
Страницы: 1 2 3 4