Рассеивание - случайная величина
Cтраница 3
Дисперсия так же, как и среднее квадратическое отклонение, является важнейшей характеристикой рассеивания случайных величин. [31]
Среднее арифметическое отклонение, наряду с дисперсией и средним квадратнческим отклонением, иногда применяется как характеристика рассеивания случайной величины. [32]
Таким образом, величина аг в значительной мере определяет вероятность тех или иных отклонений случайной величины от ее математического ожидания и характеризует рассеивание случайной величины. [33]
Существенное значение при расчете точности механизма имеет выбор величины г. В формуле ( 15) радикал соответствует средней квадратической ошибке положения механизма и для получения предельного случайного значения этой ошибки умножается на г. Теоретическая зона рассеивания случайной величины, подчиняющейся нормальному закону рассеивания, бесконечна, но вероятность получения весьма больших отклонений очень мала. [34]
Средние величины не учитывают рассеивание вокруг них отдельных значений. Для описания рассеивания случайных величин на практике применяют ряд характеристик. Простейшей характеристикой является размах ( R), применяемый для приблизительной оценки рассеивания. [35]
Математическое ожидание представляет собой некоторое среднее значение случайной величины. Дисперсия дает числовую характеристику степени рассеивания случайной величины. [36]
Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. Теоретическая схема, отображающая реальные условия возникновения рассеивания случайной величины, подчиняющейся нормальному закону распределения, лежит в основе центральной предельной теоремы теории вероятностей. Этой теоремой доказано, что случайная величина, являющаяся суммой достаточно большого числа независимых ( или слабозависимых) случайных величин, подчиненных каким угодно законам распределения, приближенно подчиняется нормальному закону распределения, и это выполняется тем точнее, чем большее количество случайных величин суммируется. [37]
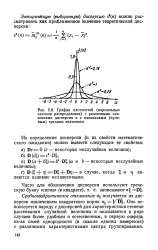 |
График плотностей ( нормальных законов распределения с различными значениями дисперсии и с одинаковым ( нулевым средним значением. [38] |
Среднеквадратическое отклонение 0 % получается из дисперсии извлечением квадратного корня а. Оно используется наряду с дисперсией для характеристики степени рассеивания случайной величины и оказывается в ряде случаев более удобным и естественным, в первую очередь из-за своей однородности ( в смысле единиц измерения) с различными характеристиками центра группирования. [39]
Среднее значение х определяет положение центра группирования или центра рассеивания случайной величины ( см. ось на фиг. [40]
Среднее значение l х определяет положение центра группирования или центра рассеивания случайной величины ( см. ось на фиг. [41]
При числе наблюдений свыше 15 - 25 рассеивание отклонений случайной величины от центра группирования характеризуется средним квадратическим отклонением а. При малом числе наблюдений ( 10 - 15 и меньше) рассеивание случайных величин целесообразно характеризовать не а, а диапазоном рассеивания R. Остаточной погрешностью называется разность между размером, полученным в результате измерения, и средним арифметическим размером, который принимается за наиболее вероятный размер детали. [42]
При извлечении корня берется только положительное значение, так как а представляет собой положительную величину. Среднее квадратическое отклонение случайных величин является наиболее важной характеристикой их рассеивания, от которой зависит величина поля рассеивания случайных величин. [43]
Во все уравнения для оценок погрешностей при изменении входят параметры автокорреляционной функции а и со, которые могут быть определены из экспериментально полученных реализаций случайной функции изменения потенциала вдоль исследуемого сооружения и, следовательно, являются статистическими оценками. Однако, как это следует из формул ( 31) и ( 41), среднее квадратическое отклонение, характеризующее рассеивание случайной величины вокруг истинного математического ожидания этой величины, уменьшается в 1 / п раз с увеличением числа реализаций п, по которому производится усреднение. Все сказанное в полной мере относится к оценке погрешностей а и со. [44]
Сущность этого способа состоит в том, что в плоскости, параллельной шкале, помещается зеркальная плоскость, отражающая стрелку указа-геля. Наблюдатель становится в такое положение, чтобы изображение указателя в зеркале и сам указатель совпадали. Пэпутно укажем, что точность отсчета имеет большое значение и при определении характеристик рассеивания случайных величин, так как при относительно низкой точности отсчета получается ( при любом числе наблюдений) малое число значений случайной величины ( меньше шести), что затрудняет или делает вовсе невозможной обработку результатов наблюдений ( см. гл. [45]
Страницы: 1 2 3 4