Многократное рассеяние

Cтраница 1

Многократное рассеяние приводит к возникновению на МДК экстра-рефлексов, если луч, дифрагированный на одном семействе плоскостей, может вторично дифрагировать на другом семействе плоскостей ( с иным межплоскостным расстоянием) или на плоскостях того же семейства, но несколько иначе ориентированных; экстра-рефлексы часто возникают на МДК от двойниковых и двухфазных структур, что усложняет анализ таких МДК, по-сколько создается ложное впечатление о периодичности, в действительности не существующей. [1]

Многократное рассеяние может быть использовано для определения размера областей неоднородности. При этом вместо построения кривых рассеяния для образцов различной массы применяют определение интенсивности прямого пучка при различных положениях образца. [2]

Многократное рассеяние излучения учитывается введением в общее выражение сомножителя, называемого фактором накопления В. [3]

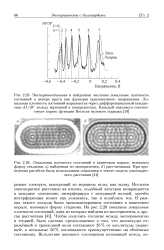
Диаграмма уровней энергии гармонического осциллятора. [4]

Многократным рассеянием электронов на молекулах СО можно пренебречь, поскольку интенсивность электронного потока е и плотность молекул СО сравнительно низки. [5]

Экспериментальная и найденная численно локальные плотности состояний в центре круга как функции приложенного напряжения. Локальная плотность состояний выражается через дифференциальный кондак-тане dl / dV между вершиной и поверхностью. Каждый максимум соответствует корню функции Бесселя нулевого порядка.| Локальная плотность состояний в квантовом корале, имеющем форму стадиона. а найденная из эксперимента, б рассчитанная. При проведении расчетов была использована описанная в тексте модель многократного рассеяния. [6]

Испытав многократное рассеяние на атомах, подобный электрон возвращается в исходное положение, интерферируя с исходящей волной, причем интерференция может как усиливать, так и ослаблять ток. В рамках такого подхода были проанализированы состояния в квантовом корале, имеющем форму стадиона. Чтобы получить согласие между экспериментом и теорией, было сделано предположение о том, что амплитуды отраженной и прошедшей волн составляют 25 % от амплитуды падающей, а остальные 50 % поглощаются преимущественно на объемных состояниях. [7]

Хотя многократное рассеяние происходит по тем же законам, что и однократное, расчет интенсивности света, прошедшего через плотное облако, представляет значительные математические трудности. Точное решение получено только для весьма идеализированных условий, в основном для изотропного рассеяния и для случаев точечного источника света и сферических рассеивающих систем, а также плоского источника и плоскопараллельных систем. [8]

Явление многократного рассеяния сказывается двояко на результатах эксперимента по определению коэффициента поляризации. Во-вторых, заряженные частицы, не испытавшие ни одного ядерного столкновения, отклоняются от своего первоначального пути вследствие многократного рассеяния. Так как многократное рассеяние характеризуется равномерным распределением рассеянных частиц по углу ф, то регистрация заряженных частиц, не испытавших рассеяния на одном из ядер мишени, приводит к заниженному значению коэффициента поляризации. [9]

Теория многократного рассеяния в сплошных средах наиб, хорошо развита для случая одномерных неодно-родностей, а в трехмерно-неоднородных средах - в приближении малоуглового рассеяния вперед. Для анализа используются схема марковских случайных процессов в диффузионном приближении, теория переноса излучения, метод суммирования ряда теории возмущений по кратности рассеяния при помощи фейнма-новских диаграмм ( решения Дайеона уравнения и Бете - Солпитера уравнения), метод геом. Одним из наиб, ярких эффектов многократного рассеяния в одномерной среде является полное отражение волны от цолуоесконечной среды со слабыми флуктуациями показателя преломления. При малоугловом многократном рассеянии в среде с трехмерными неоднородностями происходит накопление флуктуации параметров волны с ростом дистанции. В частности, накопление с расстоянием флуктуации направления нормали к поверхности пост, фазы волны приводит к росту ширины угл. В среде с пространственно-временными неоднородностями аналогичным образом растет с расстоянием ширина частотного спектра. Дисперсия флуктуации интенсивности на нек-рой глубине выходит на стационарный уровень. Совместное влияние диссипации и рассеяния приводит к существованию глубинного режима, когда угл. [10]

Рассеяние волн от поверхности кристалла. Черные кружки показывают положение атомов. большими кружками обведены тех из них, на которых происходит рассеяние, ( а Рассеяние одиночным атомом. Такое событие адекватно описывается кинематической теорией. Дифракция возникает тогда, когда волна, отмеченная пунктирной линией, складывается в фазе с волной, отмеченной сплошной линией. ( Ь Рассеяние парой атомов. Вперед рассеянный луч kg рассеивается на втором атоме, создавая лучи k и k 2. которые складываются с лучами k t и k 2, созданными при первом рассеянии, ( с Случай парного рассеяния. сейчас уже k - волновой вектор поверхностной волны. [11]

Существование значительного многократного рассеяния можно продемонстрировать экспериментально двумя разными способами. [12]

Теория многократного рассеяния света чрезвычайно близка к теории переноса нейтронов. [13]

При многократном рассеянии света в атмосфере и отражении от поверхности планеты происходит потеря информации о величинах, определяющих искомые оптич. Для получения однозначного решения приходится вводить значительные упрощающие допущения, сильно ограничивающие возможности исследования. [14]

Как учитывается многократное рассеяние в программе обработки. [15]

Страницы: 1 2 3 4