Многократное рассеяние

Cтраница 3

Борна для однократного, двукратного и многократного рассеяния на плоскостях в кристалле. Использовав другие методы, Фудзимото [145] и Фудзивара [149] получили тот же результат, но в несколько более общей форме, в которой г-компоненты волновых векторов для отдельных отражений включены в знаменатели, чтобы учесть небольшие отличия в направлении соответствующих волн. [31]

Грае 0 3 многократное рассеяние играет существенную роль. [32]

Излучение, испытавшее многократное рассеяние, обычно не удается полностью устранить, однако его можно обнаружить, измеряя интенсивность при различных длинах волн падающего света. [33]

Для оценки эффектов многократного рассеяния полезна модель, предложенная Коэном. Данная модель основывается на применении схемы Вигнера - Зейтца к электрону в кристалле гелия. Каждый атом гелия представляется как твердая сфера с радиусом, равным длине рассеяния. [34]

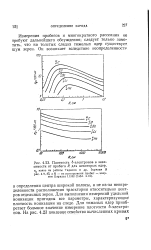Плотность 6-электронов в зависимости от пробега R для некоторых ядер. [35]

Измерения пробегов и многократного рассеяния не требуют дальнейшего обсуждения; следует только заметить, что на толстых следах тяжелых ядер существует шум зерен. [36]

Давайте рассмотрим случай многократного рассеяния на системе массивных нуклонов. Основное предположение теории многократного рассеяния состоит в том, что свойства каждого рассеи-вателя не меняются из-за присутствия других рассеивателей. [37]

Одним из следствий многократного рассеяния является искажение профиля акустического пучка, вызванное флуктуациями показателя преломления. [38]

Функция Шермана для золота при анергии электронов 0 0 1 МэВ и 2 0 МэВ. [39]

Для исключения влияния многократного рассеяния электронов на меньшие углы при том же результирующем угле ft необходимо использовать мишени с относительно небольшой плотностью атомов. Hg ( мишень) должна соответствовать давлению р 10-а мм рт. ст.; толщина золотой фольги, используемой в детекторах Мотта, не должна превышать 100 нм. [40]

В классической теории многократного рассеяния света делаются два основных предположения. Во-первых, считается, что воздействием излучения на среду, в которой оно распространяется, можно пренебречь. Тем самым обеспечивается линейность уравнения переноса. Во-вторых, предполагается, что взаимодействие излучения и вещества не приводит к изменению частоты квантов. Однако существует множество задач, где оно является очень хорошим приближением к действительности. В качестве примера можно указать на проблемы многократного рассеяния света на частицах, размеры которых сравнимы с длиной волны излучения. Условие применимости предположения о неизменности частоты состоит в том, что в спектральном интервале, охватывающем возможные частоты кванта как до, так и после рассеяния, оптические свойства среды меняются мало. [41]

Величина 6 обязана многократному рассеянию. [42]

Описанное явление называется многократным рассеянием. [43]

Близкая связь между многократным рассеянием и торможением при ядерных столкновениях дает, как уже упоминалось, средство установить ту роль, которую играют эти столкновения при прохождении частицы через вещество. Для этой цели существенно, что электронные столкновения, хотя часто и оказывают доминирующее влияние на торможение, обычно играют второстепенную роль для рассеяния. Для частиц с малыми скоростями, как вытекает из рассуждений, которые будут приведены в гл. [44]

Свет, обусловленный многократным рассеянием, который падает на рассеивающий объем V, имеет всевозможные направления. Кроме того, многократное рассеяние является некогерентным рассеянием. [45]

Страницы: 1 2 3 4