Рассмотрение - дифференциальное уравнение
Cтраница 1
Рассмотрение дифференциальных уравнений и связанных с ними задач электротехники в случаях, когда правая часть уравнения ( 72) не допускает преобразования Фурье, но имеет преобразование Лапласа, будет произведено в следующей главе. [1]
После рассмотрения дифференциальных уравнений движения и двух основных задач динамики несвободной материальной системы изучается метод Лагранжа. [2]
После рассмотрения дифференциальных уравнений движения и двух основных задач динамики несвободный материальной системы изучается метод Лагранжа. Вводится понятие об обобщенных координатах, обобщенных скоростях и обобщенных силах. Выводятся общее уравнение статики в обобщенных координатах и уравнения равновесия несвободной материальной системы. Уравнения движения в обобщенных координатах вытекают из уравнений равновесия и принципа Даламбера-Для этого достаточно к обобщенной активной силе добавить обобщенную силу инерции. [3]
При рассмотрении дифференциальных уравнений, описывающих какой-либо физический процесс, необходимо учитывать, что сами эти уравнения и начальные условия для разыскиваемых решений обычно бывают известны лишь приближенно. [4]
При рассмотрении дифференциальных уравнений, особенно нелинейных, на римановых поверхностях и в других вопросах приходится иметь дело с переменными поверхностями, пробегающими некоторое их семейство. [5]
При рассмотрении дифференциального уравнения Риккати (1.1) целесообразно отметить следующий важный факт. [6]
Уже при рассмотрении дифференциального уравнения второго порядка ( п - 2) выяснилось, что наличие равных нулей требует особого подхода; поэтому и здесь мы рассмотрим этот случай отдельно. [7]
Обратимся теперь к рассмотрению дифференциального уравнения ( 116) в том случае, когда разности ( Вх - С) и ( Ву - С) противоположных знаков и, следовательно, коэффициент при Мх в уравнении ( 116) отрицателен. [8]
В то же время при рассмотрении дифференциальных уравнений переход от одномерного случая ( обыкновенные уравнения) к многомерному ( уравнения с частными производными) требует совершенно других подходов и методов решения. [9]
В то же время при рассмотрении дифференциальных уравнений переход от одномерного случая ( обыкновенные уравнения) к многомерному ( уравнения с частными производными) требует совершенно других подходов и методов решения. [10]
Решения чаще всего основываются на рассмотрении дифференциального уравнения движения установившегося турбулентного потока, но различаются по условиям на границах водоема. В решении А. В. Караушева [73], например, скорость потока на дне принята равной некоторому конкретному значению, что соответствует так называемому условию скольжения потока. Результаты расчета распределения скорости по вертикали, полученные с использованием метода Караушева применительно к оз. [11]
Статический метод исследования устойчивости основан на рассмотрении дифференциальных уравнений равновесия деформируемой системы в момент, соответствующий бифуркации форм ее равновесия, причем эти уравнения составляются для искривленной формы равновесия. Их решение позволяет установить форму потери устойчивости и определить величины критических нагрузок. [12]
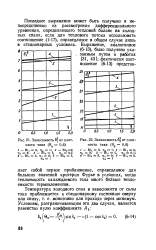 |
Зависимость 6 от плот - Рнс. 22. Зависимость 6 от плот. [13] |
Последнее выражение может быть получено и непосредственно из рассмотрения дифференциального уравнения, определяющего тепловой баланс на холодных спаях, если для теплового потока использовать соотношение ( 1 - 17), справедливое в общем случае лишь в стационарных условиях. [14]
При такой постановке задачи расчет преобразователя сводится к рассмотрению дифференциального уравнения теплопроводности стенки преобразователя с граничными условиями третьего рода между стенкой преобразователя и газовым потоком, а также между теплоизолированной стенкой преобразователя и окружающей средой. Следует отметить, что учет теп-лопотерь в окружающую среду имеет весьма существенное значение, особенно при измерении расходов газов неконтактным тепловым методом. [15]
Страницы: 1 2 3