Расстояние - хэмминг
Cтраница 1
Расстояние Хэмминга dH ( a b) между двумя элементами а и b из G есть число координат, в которых они различаются, или, что то же, dH ( a, b) есть вес Хэмминга разности а - b в G. Пусть a, b - элементы из G, находящиеся на заданном расстоянии dH ( a b) k друг от друга. [1]
Расстояние Хэмминга является метрикой, а куб Вп - метрическим пространством. [2]
Расстояние Хэмминга тесно связано с вероятностью ошибки при передаче сообщения. [3]
Расстояние Хэмминга обладает многими свойствами обычного геометрического расстояния ( см., например, ниже Приложение II, стр. Поэтому важной характеристикой кода является отвечающее ему кодовое расстояние D min а - а Jx - расстояние Хэмминга между самыми близкими различными кодовыми обозначениями данного кода. [4]
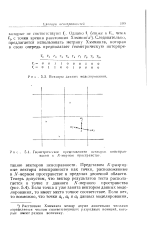 |
Векторы данных моделирования. [5] |
Расстояние Хэмминга между двумя двоичными числами определяется числом соответствующих разрядных позиций, которые имеют разную величину. [6]
Расстоянием Хэмминга d ( x, х) между двумя наборами х и х называют число компонент, в которых наборы х и х различаются. [7]
Рассмотрение расстояния Хэмминга оправдано только в случае белого шума. [8]
Определим теперь расстояние Хэмминга d ( у; х) между двумя двоичными последовательностями как число позиций, в которых отличаются эти две последовательности. [9]
Это расстояние обычно называется расстоянием Хэмминга. Оно приспособлено для двоичного белого шума. [10]
Так, для исправления одиночной ошибки расстояние Хэмминга между разрешенными кодовыми комбинациями должно быть не менее трех. [11]
В этом случае перекрытие просто зависит от расстояния Хэмминга daP, которое показывает долю несовпадающих знаков двух JV-значных двоичных чисел. [12]
В книге используются обычные названия коды Хэмминга и расстояние Хэмминга; использование здесь других терминов было бы проявлением ложной скромности и лишь запутало читателя. [13]
Расстояниями кода называются ненулевые значения, действительно принимаемые расстоянием Хэмминга между кодовыми словами. Параметр s кода, определенный в разд. [14]
Далее устанавливается связь между энтропийной метрикой и математическим ожиданием расстояния Хэмминга. [15]
Страницы: 1 2 3 4