Расстояние - хэмминг
Cтраница 2
Единственное отличие состоит в том, что здесь не используется расстояние Хэмминга. Поэтому рассмотрим мягкое декодирование, осуществляемое с евклидовым кодовым расстоянием. На рис. 7.22, г показана первая секция решетки кодирования, которая вначале имела вид, приведенный на рис. 7.7. При этом кодовые слова преобразованы из двоичных в восьмеричные. [17]
Таким образом, в этом случае приемник максимального правдоподобия работает по расстоянию Хэмминга. Это справедливо также в случае белого шума для любого кода: минимальное расстояние Хэмминга задает приемник максимального правдоподобия. В случае, если на одинаковом расстоянии находится более двух сообщений, по-прежнему можно выбирать сообщение методом случайного выбора. [18]
При изучении корректирующих кодов очень полезно понятие о кодовом расстоянии или расстоянии Хэмминга. Расстоянием d между двумя кодовыми комбинациями называют число позиций, в которых эти комбинации имеют разные символы. Расстояние между различными комбинациями некоторого конкретного кода может быть различным. [19]
Интересным моментом в них явился новый вид кодового расстояния, отличный от расстояния Хэмминга. [20]
На рис. 6.13 расстояние между двумя кодовыми словами U и V показано как расстояние Хэмминга. Каждая черная точка обозначает искаженное кодовое слово. На рис. 6.13, а проиллюстрирован прием вектора гь находящегося на расстоянии 1 от кодового слова U и на расстоянии 4 от кодового слова V. [21]
Начиная из первой ветви, декодер вычисляет 2L ( восемь) совокупных метрик путей расстояния Хэмминга и решает, что бит для первой ветви является нулевым, если путь минимального расстояния содержится в верхней части дерева, и единичным, если путь минимального расстояния находится в нижней части дерева. [22]
Фишер [170] изучает булево векторное пространство с метрикой Хэмминга, обращая основное внимание на классификацию векторов относительно расстояния Хэмминга. [23]
Для простоты предположим, что мы имеем дело с каналом BSC; в таком случае приемлемой мерой расстояния будет расстояние Хэмминга. Кодер для этого примера показан на рис. 7.3, а решетчатая диаграмма - на рис. 7.7. Для представления декодера, как показано на рис. 7.10, можно воспользоваться подобной решеткой. Поскольку в этом примере возможны только два перехода, разрешающих другое состояние, для начала не нужно показывать все ветви. Принцип работы происходящего после процедуры декодирования можно понять, изучив решетку кодера на рис. 7.7 и решетку декодера, показанную на рис. 7.10. Для решетки декодера каждую ветвь за каждый временной интервал удобно пометить расстоянием Хэмминга между полученным кодовым символом и кодовым словом, соответствующим той же ветви из решетки кодера. Как показано на рис. 7.3, кодер характеризуется кодовыми словами, находящимися на ветвях решетки кодера и заведомо известными как кодеру, так и декодеру. Эти слова являются кодовыми символами, которые можно было бы ожидать на выходе кодера в результате каждого перехода между состояниями. Пометки на ветвях решетки декодера накапливаются декодером в процессе. Другими словами, когда получен кодовый символ, каждая ветвь решетки декодера помечается метрикой подобия ( расстоянием Хэмминга) между полученным кодовым символом и каждым словом ветви за этот временной интервал. Глядя вновь на решетку кодера, видим, что переход между состояниями 00 - 10 порождает на выходе кодовое слово 11, точно соответствующее полученному в момент г, кодовому символу. В итоге, метрика входящих в решетку декодера ветвей описывает разницу ( расстояние) между тем, что было получено, и тем, что могло бы быть получено, имея кодовые слова, связанные с теми ветвями, с которых они были переданы. По сути, эти метрики описывают величину, подобную корреляциям между полученным кодовым словом и каждым из кандидатов на роль кодового слова. В алгоритме декодирования эти метрики расстояния Хэмминга используются для нахождения наиболее вероятного ( с минимальным расстоянием) пути через решетку. [24]
ЛП ( С)), где Лг - ( С) обозначает среднее число кодовых слов, находящихся на расстоянии Хэмминга i от фиксированного кодового слова. [25]
Второй член является суммой по всем непосланным кодовым словам, каждое из которых может оказаться в шаре радиуса г, который ( по отношению к п) несколько больше расстояния Хэмминга, соответствующего среднему числу ошибок. Можно надеяться, что после случайного выбора сообщений они так распределятся по всему пространству, что вероятность того, что в шаре окажется другое сообщение, будет очень мала. Это происходит вследствие того, что - мерное пространство очень просторно: вероятность того, что две случайные точки в пространстве большой размерности окажутся близкими друг к другу, очень мала. [26]
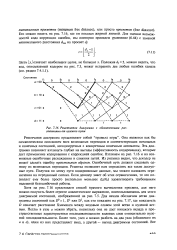 |
Решетчатая диаграмма с обозначенными расстояниями от нулевого пути. [27] |
Хотя на рис. 7.16 представлен способ прямого вычисления просвета, для него можно получить более строгое аналитическое выражение, воспользовавшись для этого диаграммой состояний, изображенной на рис. 7.5. Для начала обозначим ветви диаграммы состояний как D I, D или D2, как это показано на рис. 7.17, где показатель D означает расстояние Хэмминга между кодовым словом этой ветви и нулевой ветвью. Петлю в узле а можно убрать, поскольку она не дает никакого вклада в пространственные характеристики последовательности кодовых слов относительно нулевой последовательности. Более того, узел а можно разбить на два узла ( обозначим их а и е), один из них представляет вход, а другой - выход диаграммы состояний. [28]
При заданном конечном множестве Y совокупность Y всех последовательностей длины п с элементами из Y иногда рассматривают как метрическое пространство с метрикой Хэмминга. Напомним, что расстояние Хэмминга между двумя последовательностями длины п равно числу позиций, в которых эти две последовательности не совпадают. [29]
Расстояние Хемминга между двумя последовательностями равной длины соответствует числу позиций, занятых несовпадающими элементами. В случае последовательностей различной длины расстояние Хэмминга определяется как минимальное число позиций, занятых несовпадающими элементами при. [30]
Страницы: 1 2 3 4
