Предыдущее рассуждение
Cтраница 2
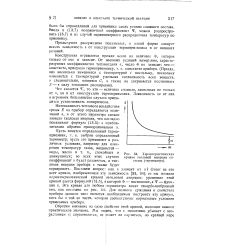 |
Характеристическая кривая тепловой инерции системы ( термометра. [16] |
Предыдущее рассуждение показывает, в какой форме следует искать зависимость s от конструкции термоприемника и от внешних условий. [17]
Предыдущее рассуждение предполагает, что полезность - понятие субъективное. Полезность одного и того же конкретного продукта для разных людей совершенно различна. Так, бутылка дешевого крепленого вина, вполне вероятно, обладает весьма значительной полезностью для опустившегося алкоголика, но нулевой или даже отрицательной полезностью для председателя местного общества трезвости. Для любого, кто страдает сильной близорукостью или дальнозоркостью, очки имеют огромную полезность, однако человек со 100 % - ным зрением не обнаружит в них для себя вовсе никакой полезности. [18]
Предыдущее рассуждение никак не зависит от топологии кластеров - они могут быть петлями, интервалами, деревьями или чем-нибудь еще. [19]
Предыдущее рассуждение можно заменить ссылкой на теорему Тихонова: если пространство / наделить произведением дискретных топологий сомножителей, то множества Jp образуют убывающую последовательность непустых замкнутых множеств. [20]
Согласно предыдущим рассуждениям можно считать, что G имеет не менее пяти вершин. Легко проверить, что для таких графов все реберные изоморфизмы индуцируются вершинными изоморфизмами. [21]
Аналогично предыдущим рассуждениям определим сближение ( перемещение) конца трубы длиной 2 / при укладке ее в спираль. [22]
Согласно предыдущим рассуждениям можно считать, что G имеет не менее пяти вершин. Легко проверить, что для таких графов все реберные изоморфизмы индуцируются вершинными изоморфизмами. [23]
Предыдущими рассуждениями эту теорему можно считать установленной лишь в случае, если функция со ( д -) имеет непрерывные вторые производные. [24]
Предыдущими рассуждениями осуществлен незаметный переход от функций, зависящих от положения, к функциям времени. Покажем, что такой переход корректен. [25]
Предыдущим рассуждением мы доказали, что интеграл Лебега существует для всякой функции, ограниченной и измеримой на множестве конечной меры. [26]
Повторяя предыдущее рассуждение, мы найдем в пространстве С 2 1 такой базис, что идеал / m j будет содержать отмеченный полином по последней координате хт 1 этого базиса. [27]
Но предыдущее рассуждение вовсе не показывает, что должна суще-твовать тригонометрическая сумма б п ( б), принимающая произвольно заданные значения Sn ( 0), Sn ( a. [28]
Но предыдущее рассуждение не дает возможности установить верхние границы модулей последовательных производных z внутри малого круга а. Можно было бы устранить это затруднение, не вводя нового принципа, а применяя то же рассуждение к окружности С1у заключающей кружок а ( так как мы знаем благодаря предыдущему верхние границы модулей производных первых п порядков на окружности С), но имеющей свой центр вне а. Надо иметь в виду, что возникающее затруднение, которое состоит в том, что внутри а будут ограничены только производные п - 3 первых порядков, будет незначительным. Однако, если желательно оставить лемму в той формулировке, в которой она была дана, то нужно поступить иным образом. С этой целью можно было бы использовать метод вспомогательных функций, как это было сделано в моей русской статье, но проще применить метод последовательных приближений который мне послужил, для доказательства основной теоремы об аналитической природе решений. [29]
Все предыдущее рассуждение опирается на недоказанное нами предложение, что действие Земли на находящиеся на ее поверхности материальные точки таково, как если бы вся масса Земли была сосредоточена в ее центре. [30]
Страницы: 1 2 3 4