Раствор - циркуль
Cтраница 1
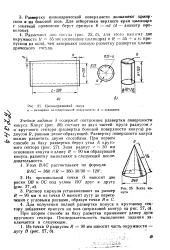 |
Цилиндрический сосуд..| Эскиз конуса. [1] |
Раствор циркуля устанавливают на размер R 90 мм и из точки О наносят дугу до пересечения с угловыми рисками, образуя точки В и С. [2]
Раствором циркуля, равным радиусу окружности, делаем на ней засечки в точках А, В, С, D, E, F. Соединяя точки А, В, С, D, E, F подряд, получим правильный шестиугольник. [3]
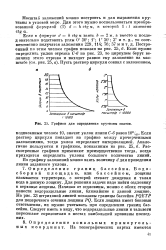 |
Графики для определения крутизны скатов. [4] |
Если раствор циркуля попадает на графике между прочерченными заложениями, тогда уклон определяют интерполяцией. Рассмотренные графики применяют преимущественно тогда, когда приходится определять уклоны большого количества линий. [5]
Установить раствор циркуля, равный длине отрезка АВ. [6]
 |
Рамка и координатная сетка листа карты масштаба 1. 10 000. [7] |
Если раствор циркуля попадет на графике между прочерченными заложениями, тогда уклон определяют интерполяцией. Рассмотренные графики применяют преимущественно тогда, когда приходится определять уклоны большого количества линий. [8]
Далее раствором циркуля, равным ВС, из каждого деления окружности засекаем эквидистантную кривую и получаем Ci, Сг, Cs... [9]
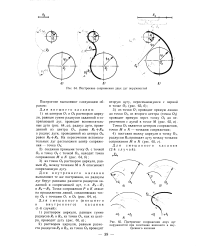 |
Построение сопряжения двух дуг окружностей.| Построение сопряжения двух дуг. [10] |
Оз раствором циркуля, равным з, между точками М я N описывают сопрягающую дугу. [11]
Далее раствором циркуля, равным ВС, из каждого деления окружности засекаем эквидистантную кривую и получаем Ci, Сг, Cs... [12]
Далее раствором циркуля, равным ВС, из каждого деления окружности засекаем эквидистантную кривую и получаем точки С ], С-2, Сз... [13]
При уменьшении раствора циркуля е число отрезков, необходимых для того, чтобы аппроксимировать кривую, возрастает. [14]
Геометрия одного раствора циркуля должна быть поэтому понимаема только в том смысле, что допускается и проведение прямых линий, причем делают построения возможно более простыми. [15]
Страницы: 1 2 3 4