Раствор - циркуль
Cтраница 2
 |
Построения прямых углов с помощью угольника. [16] |
Не меняя раствора циркуля, делают засечки из точек пересечения дуги со сторонами угла. Через полученные точки М и N и вершину угла проводят прямые. [17]
Тем же раствором циркуля от одной из точек пересечения прямой и окружности ( на рис. 5.65 точка М) откладываем на прямой АВ в любую сторону отрезок MN. Снова тем же раствором засекаем из точки N точку окружности D. Через точки С и D проводим прямую. Это и есть искомая прямая. [18]
Далее следует установить раствор циркуля на размер хп и отложить на окружности п равных частей. [19]
Для нахождения величины раствора циркуля приспособление устанавливают таким образом, чтобы расстояние между точками 6 ( R) на обоих линейках было равно радиусу делимой окружности. [20]
Таким образом, раствором циркуля не представляется возможным взять размер длины образующей. [21]
С, то меняют раствор циркуля и снова делают засечки до тех пор, пока не добьются совпадения засечек в точке С. После этого в точках В и С ставят керны. [22]
 |
Сравнение чертежа в трех видах и аксонометрической проекции. [23] |
Чему должен быть равен раствор циркуля при делении окружности на шесть равных частей. [24]
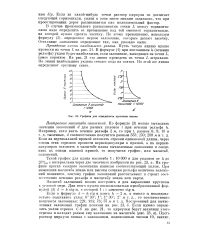 |
Графики для определения крутизны скатов. [25] |
Если из какой-нибудь точки раствор циркуля не достигает следующей горизонтали, уклон в этом месте меньше заданного, что при проектировании дорог расценивается как положительный фактор. [26]
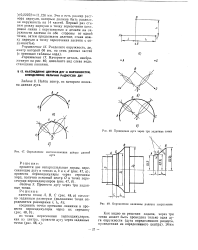 |
Определение местоположения центра данной дуги.| Проведение дуги через три заданные точки.| Определение величины радиуса закругления. [27] |
Это и есть размер раствора циркуля, которым должна быть разделена окружность на 1.4 частей. Первый раз ставим ножку циркуля в точку пересечения центровой линии с окружностью и делаем на окружности засечки по обе стороны от одной точки, затем продолжаем деление, ставя ножку циркуля в точку пересечения засечки с окружностью. [28]
Тогда из вершины С раствором циркуля, равным длине данной диагонали, строим точку D на гипотенузе АВ. Получим прямоугольник DECF с данной диагональю CD. Пусть h - высота, проведенная из вершины С на гипотенузу. Если CD h, то задача имеет единственное решение; если CD h, то решения два; а если CD / г, то решения нет. [29]
Следует производить построения с растворами циркуля, меньшими 60, так как при больше. [30]
Страницы: 1 2 3 4