Значение - определенный интеграл
Cтраница 2
Алгоритм вычисления значения определенного интеграла с задаваемой точностью s 0 должен быть оформлен в виде описания процедуры. [16]
На вычисление значения определенного интеграла от заданной аналитически функции fW по формуле трапеций численного интегрирования требуется 7 2 Wf условных арифметических операций, где vfy - число условных арифметических операций в аналитическом выражении функции. [17]
На вычисление значения определенного интеграла по формуле Симпсона требуется 9 3 и условных арифметических операций, где wf - число условных арифметических операций аналитического выражения функции. [18]
Этим фактически найдено значение определенного интеграла, составляющего правую часть этого равенства. [19]
Лобачевский иногда находит значение сложного определенного интеграла, иногда приводит одни интегралы к другим. Он дает таким образом приложение воображаемой геометрии к анализу. Мемуар заканчивается таблицей, содержащей сравнение интегралов и найденные вновь определенные интегралы. Впрочем, в самом заключении Лобачевский отмечает еще один очень важный факт. [20]
Именно, сравниваются значения нек-рых определенных интегралов ( наз. Наиболее общим из них является принцип, установленный У. Hamilton, 1834 - 35) для случая стационарных голономных связей и обобщенный М. В. Остроградским ( 1848) на нестационарные геометрич. Пусть известны положения Р0 и PI голономной системы в моменты времени ta и t в нек-ром ее действительном движении иод действием заданных сил и сил реакций. В этом движении убудут функциями времени, к-рые удовлетворяют связям и принимают для tt0 и i. При этом 6rv уничтожаются при tta и ttl и имеют смысл возможных перемещений. [21]
Полученный предел является значением определенного интеграла. [22]
Инженеру часто приходится вычислять значения определенного интеграла численными методами. Это бывает в тех случаях, когда либо не удается выразить интеграл в замкнутой форме, либо она настолько сложна, что проще воспользоваться численным интегрированием. Как было показано выше ( рис. 8.3), численное интегрирование представляет собой устойчивый процесс. В противоположность численному дифференцированию оно уменьшает влияние погрешностей в исходных данных на окончательный результат. В основе численного интегрирования лежит приближенное вычисление площади под кривой, описываемой подынтегральной функцией. [23]
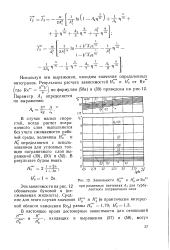 |
Зависимости Яп. [24] |
Используя эти выражения, находим значения определенных интегралов. [25]
Вычислить и вывести на печать значения определенного интеграла методами трапеций и Симпсона. [26]
Формула Тейлора позволяет приближенно вычислять и значения определенных интегралов. Рассмотрим один пример такого. [27]
Задача численного интегрирования функции заключается в вычислении значения определенного интеграла на основании ряда значений подынтегральной функции. [28]
Часто встречающаяся в инженерных расчетах процедура вычисления значения определенного интеграла сводится к определению площади, ограниченной подынтегральной кривой на участке интегрирования. Здесь предпочтение следует отдавать методу парабол, в котором подынтегральная функция аппроксимируется отрезками парабол, проведенными через три соседние точки графика функции, а приближенное значение интеграла определяется суммой площадей четырехугольников с одной криволинейной стороной. При плавных подынтегральных функциях и большой скорости вычисления интеграла ( если это вычисление участвует в многократных циклах) можно воспользоваться методом прямоугольников, когда подынтегральная функция аппроксимируется ступенчатой и интеграл находится как сумма площадей прямоугольников. В библиотеках стандартных подпрограмм обычно представлено несколько методов, но их выбор требует творческого подхода. Поэтому каждый раз следует внимательно знакомиться с математической характеристикой стандартной подпрограммы, ограничениями, накладываемыми особенностью данной ЦВМ и вычислительным методом на исходные данные. Все это приводится в паспортной части программ, включенных в библиотеку. [29]
В приведенном примере использован оператор ИНТЕГРАЛ для вычисления значения определенного интеграла по методу Симпсона. В выражении, идентифицирующем функцию, слева от знака равенства записывают две латинские буквы подряд, справа же записывают арифметические и другие действия, приводящие к вычислению функции. [30]
Страницы: 1 2 3 4