Секундный расход - жидкость
Cтраница 2
Аналогичными величинами в гидравлической и электрической системах является давление р и напряжение Е, секундный расход жидкости Q и сила тока. [16]
Здесь to - вектор скорости фильтрации в данной точке, определенный как предел отношения секундного расхода жидкости через площадку, перпендикулярную к направлению максимального расхода, к величине площадки, когда эта пеличина стремится к нулю. В круглой скобке стоит известный по гл. III трехчлен Бернулли ( V2 / 2 р / у z), который в данном случае выродился в двухчлен, так как скорость движения сквозь поры, как правило, имеет порядок нескольких миллиметров в секунду, а иногда и меньше. Вместе с тем малая скорость или, точнее, малые рейнольдсовы числа протекания вязкой жидкости сквозь поры позволяют пренебрегать конвективными ускорениями, вызываемыми кривизной пор и переменностью площади их сечений. Эти особенности пористой среды при малых числах Рей-нольдса незначительно сказываются на среднем сопротивлении пор, а тем самым и на расходной составляющей фильтрационной скорости. Вот в чем заключается причина столь глубокого сходства закона Дарси ( 156), выведенного на основании обработки опытных материалов и представляющего по существу результат пространственного осреднения движений вязкой жидкости по случайно ориентированным и разнообразным по геометрической форме порам фильтрующей среды, и законами строго определенных движений той же жидкости в тонкой щели между параллельными плоскостями. [17]
Здесь b - вектор скорости фильтрации в данной точке, определенный как предел отношения секундного расхода жидкости через площадку, перпендикулярную к направлению максимального расхода, к величине площадки, когда эта величина стремится к нулю. В круглой скобке стоит известный по гл. III трехчлен Бернулли ( У2 / 2 р / у г), который в данном случае выродился в двухчлен, так как скорость движения сквозь поры, как правило, имеет порядок нескольких миллиметров в секунду, а иногда и меньше. Вместе с тем малая скорость или, точнее, малые рейнольдсовы числа протекания вязкой жидкости сквозь поры позволяют пренебрегать конвективными ускорениями, вызываемыми кривизной пор и переменностью площади их сечений. Эти особенности пористой среды при малых числах Рейнольдса незначительно сказываются на среднем сопротивлении пор, а тем самым и на расходной составляющей фильтрационной скорости. [18]
Здесь Ь - вектор скорости фильтрации в данной точке, определенный как предел отношения секундного расхода жидкости через площадку, перпендикулярную к направлению максимального расхода, к величине площадки, когда эта величина стремится к нулю. В круглой скобке стоит известный по гл. III трехчлен Бернулли ( V2 / 2g - f - p / Y z), который в данном случае выродился в двухчлен, так как скорость движения сквозь поры, как правило, имеет порядок нескольких миллиметров в секунду, а иногда и меньше. Вместе с тем малая скорость или, точнее, малые рейнольдсовы числа протекания вязкой жидкости сквозь поры позволяют пренебрегать конвективными ускорениями, вызываемыми кривизной пор и переменностью площади их сечений. [19]
Числитель в правой части равенства ( 124) выражает объем жидкости, вытесненный поршнем за время максимального его хода, а знаменатель - секундный расход жидкости при открытии окон золотника на величину smax. Динамическая постоянная Ts равна времени, в течение которого поршень усилителя совершает максимальный путь mmax при открытых на величину sniax окнах золотника и отключенной обратной связи. [20]
В конкретных расчетах перепад давления Ар на участке трубы длины / либо задается непосредственно, либо может быть выражен через другие заданные величины: секундный расход жидкости сквозь трубу, среднюю по сечению или максимальную скорости. [21]
В конкретных расчетах перепад давления Ар на участке трубы длины I либо задается непосредственно, либо может быть выражен через другие заданные величины: секундный расход жидкости сквозь трубу, среднюю по сечению или максимальную скорости. [22]
В конкретных расчетах перепад давления Ар на участке трубы длины I либо задается непосредственно, либо может быть выражен че - / les другие заданные величины: секундный расход жидкости сквозь трубу, среднюю по сечению или максимальную скорости. [23]
В конкретных расчетах перепад давления Др на участке трубы длины / либо задается непосредственно, либо, как далее будет показано, может быть легко выражен через другие заданные величины: секундный расход жидкости сквозь трубу, среднюю по сечению или максимальную скорость. [24]
Эта формула дает распределение скорости движения жидкости по радиусу капилляра. С ее помощью может быть определен секундный расход жидкости, протекающей через сечение капилляра. [25]
Для построения теории центробежной форсунки необходимо установить связь между коэффициентом живого сечения и геометрической характеристикой 9 / ( - 4) - При этом можно воспользоваться следующими соображениями. Из формулы ( 35) получается, что в зависимости от размеров воздушного вихря может установиться тот или иной секундный расход жидкости через форсунку. Вычисления показывают, что как при очень больших, так и при очень малых размерах воздушного вихря имеют место небольшие значения коэффициента расхода. [26]
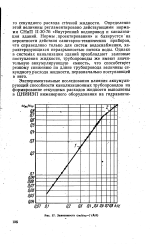 |
Зависимость ШЖ / ШТР / ( A / d. [27] |
Определение этой величины регламентировано действующими нормами СНиП И-30-76 Внутренний водопровод и канализация зданий. Однако в системах канализации зданий преобладают залповые поступления жидкости, трубопроводы же имеют значительную аккумулирующую емкость, что способствует резкому снижению по длине трубопровода величины секундного расхода жидкости, первоначально поступающей в него. [28]
Эффект ( явление) кавитации часто используется для практических целей. В том случае, когда давление в этом сечении достигнет значения, равного началу кавитации, жидкость вследствие выделения паров и газов закипает. Поскольку интенсивность кавитации и рост сопровождающего ее сопротивления повышаются с дальнейшим понижением давления, секундный расход жидкости после закипания будет сохраняться постоянным независимо от дальнейшего уменьшения давления на выходе из сопла. [29]
Страницы: 1 2