Расходимость

Cтраница 2

Расходимость при малых передаваемых импульсах, соответствующих малым углам рассеяния, связана с уже обсуждавшимся следствием дальнодействующего характера кулонов-ских сил, приводящего к бесконечному полному сечению рассеяния. [16]

Расходимость в виде обратной относительной скорости ли является характерной для экзотермической реакции. [17]

Расходимость реальных световых пучков приводит к тому, что часть лучей отклоняется от направления синхронизма, даже если ось пучка точно направлена по этому направлению. [18]

Расходимость, однако, всего лишь логарифмическая. [19]

Расходимость в данном случае носит, очевидно, чисто геометрический характер. Обозначив ее через аг, имеем ат b / pi, где Ъ - эффективная ширина источника. [20]

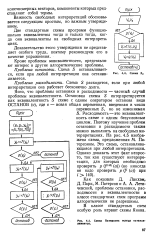Схема Патерсона всегда останавливается. [21]

Расходимость - это эквивалентность схеме с одним безусловным циклом. [22]

Расходимость, однако, всего лишь логарифмическая. [23]

Расходимость обусловленной дальними столкновениями компоненты ( Дрх) означает, что в кулоновском газе на движение частицы оказывают значительно большее влияние дальние коллективные взаимодействия по сравнению со столкновениями в ближней зоне. При-выводе уравнения Больцмана методом Трэда ( см. разд. N 2 мы должны были бы сохранить интеграл столкновений дальней зоны, а столкновительный член ближней зоны опустить. Интеграл столкновений ближней зоны дает уравнение Больцмана. [24]

Расходимость Z при В 0 означает, очевидно, отсутствие термодинамически равновесных состояний, описываемых какими-либо распределениями с отрицательной температурой. [25]

Расходимость спектров Е и ЕМ при больших k указывает на перекачку энергии в область больших волновых чисел нелинейными взаимодействиями. С другой стороны, нет оснований считать ( как бы этого нам ни хотелось), что равенство Е ЕМ указывает на тенденцию к равнораспределению в реальной турбулентности. Дело в том, что этот вопрос ( о равнораспределении) сводится к проблеме пульсационного динамо а, как это неоднократно подчеркивалось выше, динамо всегда связано с конечной диссипацией. Последней полностью пренебрегают при рассмотрении ансамбля Гиббса. [26]

Коллинеарпые расходимости, обусловленные нулевой массой конечных частиц, исчезают, если рассматривать сечение рассеяния в нек-рый телесный угол и, не фиксируя полного числа частиц и нем. Типичным примером является сечение рассеяния частицы в состояние, характеризуемое тем, что в пек-ром телесном угле Я сосредоточена доля ( 1 - е) полной энергии [ сечение Стермана - Вайпбсрга; Дж. При Й4л, е1 такое состояние представляет собой струю, образованную заряженной ( в КХД - цветной) частицей и сопровождающим ее излучением. [27]

Расходимость выражения ( 1.23 а) может быть устранена, если мы в том или ином виде учтем поле, создаваемое остальными электронами проводимости, которые экранируют поля ионов и обрезают действие кулоновского потенциала. С этой точки зрения представляется естественным сферу действия каждого рассеивающего центра ограничить половиной среднего расстояния между ионами. [28]

Расходимость первого и сходимость второго из этих рядов уже устанавливались нами дважды и в том числе при помощи интегрального признака Маклорена - Коши. Посмотрим, как работают применительно к этим рядам признаки Даламбера и Коши. [29]

Расходимость лазеров на стекле составляет - 10 мрад, что существенно ниже дифракционной. В основном это обусловлено многомодовым режимом генерации. Для уменьшения расходимости вводят ограничивающие апертуры, а также портят ( делают шероховатыми) боковые стенки стержней. Для получения мощного излучения с дифракционной расходимостью обычно используют твердотельные усилители. [30]

Страницы: 1 2 3 4