Расходимость - итерационный процесс
Cтраница 1
Расходимость итерационных процессов вблизи предела статической устойчивости при обычно используемой расчетной формуле может быть объяснена нарушением условий существования решения при регулировании мощности на поддержание узловых напряжений. [1]
Это приводит к расходимости итерационного процесса. [2]
Это и приводит к расходимости итерационного процесса. [3]
Игнорирование этого обстоятельства может ухудшить сходимость и даже привести к расходимости итерационного процесса. Матрица К2 ( S) учитывает наличие усилий в элементах при переходе от итерации к итерации. [4]
Таким образом, как метод Зейделя, так и метод простой итерации не всегда обеспечивают возможность получения решения, поскольку расходимость соответствующих итерационных процессов не исключена. Последние два фактора влияют лишь на количество итераций, необходимых для получения решения с заданной точностью. А, может привести к нарушению необходимых и достаточных условий сходимости. [5]
Однако на практике оказалось, что величины итерационных параметров, подсчитанные по формуле (1.48), не приводят к успеху и даже часто наблюдается расходимость итерационного процесса. [6]
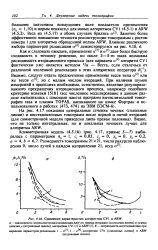 |
Сравнение характеристик алгоритмов CV1 и ARW. [7] |
Как и следовало ожидать, применение а и ( 4Э дает более быструю сходимость к точному решению, но после 3 - 5-го шага возможна расходимость итерационного процесса ( для варианта aw алгоритм CV1 фактически уже является методом Ча - Веста, если отвлечься от различной численной реализации в этих алгоритмах оператора Я, 1) - Видимо, следует отдать предпочтение применению весов типа а ( 2) или же весов а но с малым числом итераций. [8]
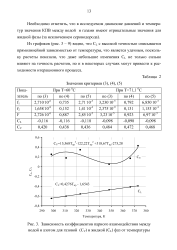 |
Значения критериев ( 3, ( 4, ( 5.| Зависимость коэффициентов парного взаимодействия между водой и азотом для газовой ( Су и жидкой ( Сь фаз от температуры. [9] |
Из графиков ( рис. 3 - 9) видно, что CL с высокой точностью описывается прямолинейной зависимостью от температуры, что является удачным, поскольку расчеты показали, что даже небольшие изменения CL не только сильно влияют на точность расчетов, но и в некоторых случаях могут привести к расходимости итерационного процесса. [10]
Решение системы уравнений математической модели ГЦ, включающей уравнение (4.92), не вызывает трудностей только при заданной ограниченной рабочей области каждого насоса. Qk Q приводит к расходимости итерационного процесса. [11]
Значение приращения нагрузки и размер сетки связаны друг с другом. Неправильный выбор любой из этих величин может привести к расходимости итерационного процесса. Чтобы наибольшее число узлов сетки разбиения находилось внутри предполагаемой пластической области, был выбран переменный шаг сетки. Сетка разбиения, используемая при условиях плоской деформации, была, как правило, более мелкой, чем сетка, используемая в случае плоского напряженного состояния. [12]
Критерий ( 8) может нарушаться лишь для систем с открытыми оболочками. Несовместность уравнений ССП в этом случае служит достаточной причиной расходимости итерационного процесса. [13]
Если будет Re ( Я -) 0 хотя бы для одного /, то при положительном h, выбираемом по (1.39), процесс итераций ( как следует из (1.38)) будет всегда расходиться. Но при этом динамический объект, которому соответствует такая система АУ, неустойчивый, поэтому расходимость итерационного процесса может служить признаком неустойчивости динамического объекта. При этом система АУ может иметь вполне определенное решение, но физически это решение будет соответствовать положению неустойчивого равновесия динамического объекта. [14]
Итерационный процесс не всегда приводит к сошедшемуся решению. Иногда значения ф колеблются от итерации к итерации или все время плывут. Такой расходимости итерационного процесса следует избегать. [15]
Страницы: 1 2