Значение - корень - характеристическое уравнение
Cтраница 1
 |
Схема АСР к приме - нением значений коэффици-ру б - 3 - ентов и требуется изменить. [1] |
Значения корней характеристического уравнения однозначно зависят от значений его коэффициентов, являющихся функциями параметров звеньев АСР. Поэтому в критериях устойчивости в той или иной форме отражаются параметры звеньев АСР, что позволяет оценивать их влияние на устойчивость системы. Известны алгебраические критерии Рауса - Гурвица и частотные критерии Михайлова и Найквиста. Все эти критерии исходят из одинаковой предпосылки и равноправны. [2]
Решение зависит от значений корней характеристического уравнения. [3]
Устойчивость структурно-устойчивых систем-определяется значением корней характеристического уравнения, которые полностью зависят от постоянных времени и коэффициентов усиления звеньев системы. [4]
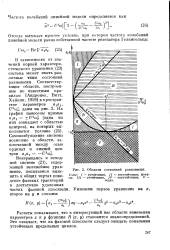 |
Области состояний равновесия. [5] |
В зависимости от значении корней характеристического уравнения ( 23) система может иметь различные типы состояний равновесия. [6]
Вполне очевидно, если известны значения корней характеристического уравнения (5.9) при любых значениях, то при некотором фиксированном значении, которое имеет исследуемая система, величины корней характеристического уравнения будут известны и, следовательно, будет выяснено является система устойчивой или неустойчивой. [7]
 |
Примеры звеньев первого порядка. [8] |
Динамические свойства звена определяют по значениям корней характеристического уравнения. Если корни комплексные, то переходный процесс имеет колебательный характер, если же корни действительные и отрицательные, переходный процесс протекает без колебаний. [9]
Устойчивость структурно-устойчивых систем полностью определяется значениями корней характеристического уравнения, которые зависят только от постоянных времени Т и коэффициентов усиления К. [10]
Затухание или незатухание компоненты полностью определяется значением соответствующего корня характеристического уравнения или полюса передаточной функции. [11]
Характер переходных процессов в линейных системах связан со значениями корней характеристических уравнений систем и функционально не зависит от начальных условий. В нелинейных системах картина иная. Здесь функционально вид переходных процессов может существенно зависеть от начальных условий. В зависимости от начальных условий переходный процесс в нелинейных системах может быть монотонным или колебательным, сходящимся или расходящимся. [12]
Характер переходных процессов в линейных системах связан со значениями корней характеристических уравнений систем и функционально не зависит от начальных условий. В нелинейных системах картина иная. Здесь функционально вид переходных процессов может существенно зависеть от начальных условий. В зависимости от начальных условий переходный процесс в нелинейных системах может быть монотонным или колебательным, сходящимся или расходящимся. Существенным отличием колебательных переходных процессов в нелинейных системах является также зависимость частоты колебаний от амплитуды. В линейных системах переходный процесс затухает до нуля или расходится до бесконечности в зависимости от того, имеют ли корни характеристического уравнения системы отрицательные или положительные вещественные части. В первом случае линейная САР является устойчивой, а во втором - неустойчивой. Суждение об устойчивости такой системы никак не связано с начальными условиями. [13]
Очевидно, судить об устойчивости системы можно, вычислив значения корней характеристического уравнения. [14]
Корневые критерии позволяют оценить качество системы в переходном режиме по значению корней характеристического уравнения. Как говорилось в § 16.4, переходный процесс в устойчивой системе определяется суммой апериодических и колебательных составляющих, число которых равно степени характеристического уравнения. [15]
Страницы: 1 2 3