Значение - корень - характеристическое уравнение
Cтраница 2
Следовательно, для суждения об устойчивости системы управления нет необходимости определять значения корней характеристического уравнения, что связано обычно с трудоемкими вычислениями. [16]
Очевидно, об устойчивости системы можно было бы судить, вычислив значения корней характеристического уравнения. [17]
Важным является то, что степень устойчивости можно найти без вычисления значений корней характеристического уравнения. [18]
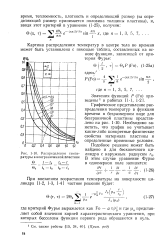 |
Распределение температуры в неограниченной пластине. [19] |
Фурье выражается как Fo a i / r и где цп представляет собой значения корней характеристического уравнения, при которых бесселевы функции первого рода обращаются в нуль. [20]
Для исследования процесса регулирования в области затухающих колебаний не обязательно, однако, знание значений корней характеристического уравнения. [21]
Затухание или незатухание переходной составляющей, а следовательно, и устойчивость системы целиком определяются значением соответствующего корня характеристического уравнения. [22]
Сущность метода заключается в графо-аналитическом определении на комплексной плоскости геометрического места точек, представляющих собой значения корней характеристического уравнения замкнутой системы при непрерывном изменении одного из ее параметров в пределах от 0 до с. Совокупность получающихся при таком изменении траекторий корней характеристического уравнения называется корневым годографом системы. В качестве переменного параметра обычно выбирают коэффициент усиления разомкнутой системы. [23]
Как уже указывалось, общее решение однородного уравнения есть сумма слагаемых, вид которых определяется значениями корней характеристического уравнения. Если в этом решении какое-нибудь его слагаемое неограниченно возрастает по абсолютной величине, то возрастает по абсолютной величине и вся сумма в целом. Принимая во внимание значения показателей степени в слагаемых (10.10) и (10.11), получаем, что присутствия одного положительного вещественного корня г - или одной пары сопряженных комплексных корней с положительной вещественной частью а / 0 оказывается достаточным, чтобы значения ус неограниченно возрастали. Следовательно, для асимптотической устойчивости движения звеньев механизма необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательную вещественную часть. [24]
В тех случаях, когда требуемая точность невысока либо когда матрица AI уравнения состояния имеет большой разброс значений корней характеристического уравнения, неявные формулы могут обеспечить существенное уменьшение числа шагов интегрирования. Однако следует иметь в виду, что эти достоинства покупаются ценой затрат, необходимых для обращения матриц в неявных формулах интегрирования. [25]
В работах А. М. Ляпунова было показано, что между устойчивостью положения равновесия исходной нелинейной системы ( 1 24) и значениями корней характеристического уравнения линеаризованной системы ( 1 27) существует следующая связь. [26]
Качество переходного процесса при определенных внешних условиях в линейных системах определяется свойствами решения однородного дифференциального уравнения динамики замкнутой системы: значениями корней характеристического уравнения и произвольными постоянными. [27]
Во-вторых, несмотря на то, что показатели экспонент в обоих случаях будут равны между собою, так как они определяются тождественными в обоих случаях значениями корней характеристического уравнения, постоянные при экспонентах различны, причем по абсолютному значению в первом случае меньше, чем во втором. Поэтому при возмущении по настройке начальная часть процесса будет идти более полого, чем при возмущении по нагрузке. Это следует иметь в виду при наладке программных регуляторов. [28]
Характер переходных процессов в линейных системах связан со значениями корней характеристических уравнений систем и функционально не зависит от начальных условий. В нелинейных системах картина иная. Здесь функционально вид переходных процессов может существенно зависеть от начальных условий. В зависимости от начальных условий переходный процесс в нелинейных системах может быть монотонным или колебательным, сходящимся или расходящимся. Существенным отличием колебательных переходных процессов в нелинейных системах является также зависимость частоты колебаний от амплитуды. В линейных системах переходный процесс затухает до нуля или расходится до бесконечности в зависимости от того, имеют ли корни характеристического уравнения системы отрицательные или положительные вещественные части. В первом случае линейная САР является устойчивой, а во втором - неустойчивой. Суждение об устойчивости такой системы никак не связано с начальными условиями. [29]
 |
Пример расположения корней на комплеко ной плоскости. [30] |
Страницы: 1 2 3