Значение - коэффициент - пуассон
Cтраница 1
 |
Изменение размеров бруса при центральном растяжении. [1] |
Значения коэффициента Пуассона для некоторых материалов даны в табл. 2.1. В результате обобщения наблюдений за деформациями упругих тел установлено, что действующее напряжение пропорционально относительной деформации. [2]
Значения коэффициента Пуассона могут быть определены или уточнены по формуле (5.9), если известна величина градиента давления гидроразрыва и другие параметры. [3]
Значение коэффициента Пуассона определяется опытным путем в результате специальных испытаний материала. [4]
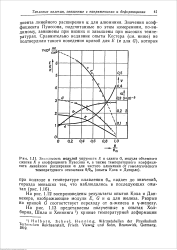 |
Зависимость модулей упругости Е и сдвига G, модуля объемного. [5] |
Значения коэффициента Пуассона, подсчитанные по этим измерениям, по-видимому, занижены при низких и завышены при высоких температурах. [6]
Значения коэффициентов Пуассона Цтах находят по (1.178) - (1.180) при замене а - н и е - н на ст-тахк и е тахк. [7]
Найти значение коэффициента Пуассона, при котором объем проволоки при растяжении не меняется. [8]
Найти значение коэффициента Пуассона, при котором объем проволоки при растяжении не меняется. [9]
Область значений коэффициента Пуассона для стекла в исследованиях Штраубеля включает весь полувековой спектр экспериментальных результатов, начиная с первых пьезометрических измерений Вертгейма в 1849 г. Даже для изотропных твердых тел коэффициент Пуассона есть функция химического состава, а также термической и механической предыстории. Трудно сказать большего или меньшего уважения заслуживает исследование, в котором достигнуты высоты точности такие, как в исследовании Штраубеля, если сравнивать последнее с зачастую более грубым первоисследо-ванием, в котором имелись и изобретательность, и оригинальность, подобно присущим исследованию Корню), однако точность и утонченность исчерпывающего исследования Штраубеля поставили перед последовавшими серьезными экспериментаторами строгие ограничения. [10]
Ниже приведены значения коэффициента Пуассона v для основных горных пород. [11]
Ниже приведены значения коэффициента Пуассона различных пород. [12]
Благодаря различию значений коэффициента Пуассона в упругой и пластической областях участки более прочного металла, работающие в упругой области, препятствуют развитию пластических деформаций в соседней мягкой прослойке. Стесненность деформаций мягкой прослойки предопределяет появление объемно-напряженного состояния и повышение сопротивления развитию в ней пластических деформаций. В результате возникает эффект контактного упрочнения мягкой прослойки, который зависит от относительной толщины прослойки к h / dvi формы поперечного сечения элемента. [13]
При некотором значении коэффициента Пуассона ( 0 2833) для цилиндра частоты сдвигового и радиального продольного резонансов совпадают. [14]
Как известно, значение коэффициента Пуассона лежит в пределах 0 ц 0 5 ( см. с. [15]
Страницы: 1 2 3 4