Значение - коэффициент - пуассон
Cтраница 4
На рис. 4 и рис. 5 приведены графики дисперсионных кривых для двух значений коэффициента Пуассона и 0 28, v 0 49 соответственно. [46]
Рассмотрим произвольную точку К на диаграмме растяжения и найдем для данной величины деформации значение коэффициента Пуассона. [47]
Если бы 40 годами раньше было известно, что для различных видов изотропного стекла значение коэффициента Пуассона меняется от 0 197 до 0 319 и что при получении этих данных точность эксперимента была более высокой чем 1 %, то, возможно, хотя и не обязательно, противоречие между атомистической теорией и континуальным экспериментом было бы меньше. [48]
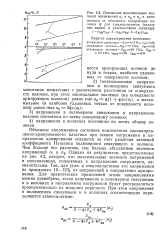 |
Отношение максимальных значений напряжений аг и а0 к az в зависимости от объемного содержания волокон ij. для стеклопластиков ( сплошные линии и углепластиков ( пунктир. [49] |
Объемное напряженное состояние компонентов однонаправ-ленно-армированного пластика при осевом нагружении в направлении армирования создается за счет различия значений коэффициента Пуассона полимерного связующего и волокон. Однако из результатов, представленных на рис. 4.2, следует, что максимальные значения напряжений в направлениях, поперечных к направлению нагружения, незначительны. Так, для угле - и стеклопластиков эти напряжения не превышают 10 - 12 % от напряжений в направлении армирования. Для практических применений этими напряжениями можно пренебречь, тогда напряжения в полимерном связующем и в волокнах в направлении нагружения будут распределяться пропорционально их модулям упругости. [50]
ЛО / р ( а - численный коэффициент, величина которого немного меньше единицы и зависит от значения коэффициента Пуассона; при ц 6 25 а 0 9194, при ц 0 5 а 0 9554) и оказывается меньше, чем скорость продольных и поперечных волн. Движение частиц в поверхностных волнах Релея происходит в плоскостях, перпендикулярных поверхности и параллельных направлению распространения. Например, при простых гармонических поверхностных волнах Релея траектория частицы представляет собой эллипс. [51]
В случае осевого нагружения в напраалении армирования 1 в компонентах монослоя создается неоднородное напряженное состояние вследствие различия значений коэффициентов Пуассона полимерного связующего и волокон. [52]
Расчетная формула по этой теории формально легко получается из выражения (3.10), ибо известно, что при значении коэффициента Пуассона [ г 0 5 деформированное тело не изменяет своего объема и, следовательно, изменяется только его форма. [53]
В полученных таким образом трех группах уравнений фигурируют три значения модуля упругости Elt Е 2, Е3 и шесть значений коэффициента Пуассона. [54]
Гипотеза о волокнистом строении при нелинейно-упругом материале и малых деформациях справедлива при постоянном ( не зависящем от напряжения) значении коэффициента Пуассона при растяжении и сжатии. Для физически нелинейных материалов техническая теории изгиба применима, если гипотезу о волокнистом строении стержней синтезировать с геометрической гипотезой плоских сечений. [55]
Страницы: 1 2 3 4