Значение - коэффициент - пуассон
Cтраница 2
Полученные двумя методами значения коэффициента Пуассона были близки между собой. [16]
Если используется такое же значение коэффициента Пуассона v 0 25, что и примененное ранее при получении точного решения, показанного на графике сплошной линией, то получаемая при этом кривая будет почти неотличима от той; что соответствует точному решению, всего лишь на один процент превышая представленные на графике значения. Как уже отмечалось в § 2.8, приближенное решение, получаемое энергетическим методом и удовлетворяющее краевым условиям, всегда несколько выше, чем точное значение критической нагрузки, но эта закономерность выполняется не всегда, если, как и в данном случае, краевые условия ле удовлетворяются. Эта важная задача является слишком специфической), чтобы обсуждать ее многочисленные особенности в книге по общей теории, но несколько замечаний Та примеров, связанных с этим, можно привести. Так же, как и в других задачах, где рассматриваются конструкции заделкой, наиболее приемлемым с тбчкй зрения практического применения является решение энергетического типа, где в работу, совершаемую внешними силами на возможных перемещениях, необходимо, разумеется, включить и работу, совершаемую нагрузкой, если таковая имеется, воспринимаемой подкрепляющими. Возможные формы потери устойчивости, которые должны рассматриваться с целью определения той, которая возникнет при наименьшем значении нагрузки, здесь более разнообразные, чем в случае неподкрепленной пластины. [17]
В табл. 42 приведены значения коэффициента Пуассона и модуля упругости материала алюминиевый сплав 1100 - волокно борсик диаметром 110 мкм. [18]
Выбирая характерные для металлов значения коэффициента Пуассона 0 3 - 0 4 и замечая, что в ГЦК решетках со а3 / 4 ( а - постоянная решетки) и радиус первой координационной сферы г № а / У-2 чжа ( 3 41) с учетом ( 3 23) находим, что для величины смещения атомов, ближайших к вакансии, в ГЦК металлах таким путем получаются значения U ( r ( 1)) - ( 0 7 - 1 6) - Ю 2 а. Внедренные в междоузлия атомы приводят к значительно большим смещениям. Например, в аустените ( раствор внедрения углерода в октаэдрические междоузлия ГЦК железа) 6F / o 1, а 0 3 и смещения ближайших атомов Fe равны 5 10 - 2 а. В случае же внедренного атома металла матрицы смещения оказываются еще больше. [19]
Если усадка из-за разности значений коэффициентов Пуассона не вносит вклад в повышенное гидростатическое давление, то остается неясным, в чем состоит причина расхождения экспериментальных и теоретических результатов. По-видимому, повышенное гидростатическое давление обусловлено тем, что в действительности упругие сферы имеют вид трещин. Уместно задаться вопросом, могут ли частицы каучука привести к достаточному объемному расширению, чтобы возросла податливость материала матрицы с температурой стеклования, скажем, 90 С и было устранено хрупкое разрушение в области температур от 23 до - 40 С. [20]
 |
Диаграмма анизотропии коэффициента Пуассона ц г д, стеклопластика ЭПС-1 с ортогональной укладкой ткани. [21] |
Этот максимум, отвечающий значениям коэффициента Пуассона, большим чем 0 5, не совпадает с диагональным направлением, а соответствует углу от 20 до 40 в зависимости от схемы армирования. [22]
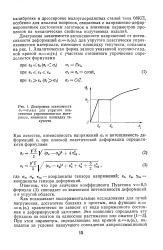 |
Диаграмма зависимости 0i CTt ( 8i для упругого пластически упрочняющегося материала, имеющего площадку текучести. [23] |
Отметим, что при значении коэффициента Пуассона v0 5 формула ( 3) совпадает со значением интенсивности деформаций и в упругой области. [24]
В 1884 г. Амага определил значения коэффициента Пуассона для резины. [25]
В табл. 80 помещены также значения коэффициента Пуассона, полученные Боком для меди, серебра и никеля. [26]
Повторение эксперимента Кирхгофа по определению значения коэффициента Пуассона, выполненное в середине XX века. [27]
Чтобы избежать усложнений из-за различия значений коэффициента Пуассона в упругой и необратимой областях деформации, примем в предыдущих уравнениях vl / 2, предполагая, что имеют место соотношения между напряжениями и скоростями необратимых деформаций, справедливые для несжимаемого материала. [28]
Разница между статическим и динамическим значениями коэффициента Пуассона невелика и может быть, вероятно, отнесена скорее к ошибкам эксперимента, чем к влиянию скорости нагру-жения. [29]
Здесь fij и р 2 - значения коэффициента Пуассона; для стали ц ж 0 3, для чугуна [ i як 0 25; значения dl и dz указаны на рис. 23.22. При нагруженкк соединения ссспой силой Ра, которая стремится вызвать осевое смещение одной детали относительно другой, на контактирующих поверхностях возникают силы трения, препятствующие этому смещению. [30]
Страницы: 1 2 3 4