Расчет - молекула
Cтраница 1
Расчет молекулы Н2 послужил убедительным доказательством применимости квантовой механики к проблеме химия, связи и показал, что силы, приводящие к образованию химич. Однако результат действия этих сил существенным образом зависит от характера распределения плотности валентных электронов в области между ядрами, к-рый, в свою очередь, в силу свойств симметрии электронной волновой функции по отношению к перестановкам пар электронов ( принцип Паули) определяется взаимной ориентацией спинов валентных электронов. [1]
Расчеты молекул показывают, что; метод ППДП / 2 по сравнению с методом ППДП дает лучшее совпадение с экспериментом. [2]
Расчет молекулы Н2 послужил убедительным доказательством применимости квантовой механики к проблеме химия, связи и показал, что силы, приводящие к образованию химия, связи, имеют в своей основе обычные силы электростатич. Однако результат действия этих сил существенным образом зависит от характера распределения плотности валентных электронов в области между ядрами, к-рый, в свою очередь, в силу свойств симметрии электронной волновой функции по отношению к перестановкам пар электронов ( принцип Паули) определяется взаимной ориентацией спинов валентных электронов. [3]
Результаты расчетов молекул XXI-XXIV приводят еще к одному интересному вопросу. Замещение в положение 8 в хи-нолине ( XXII) или в положение 5 в изохинолине ( XXIII) идет через промежуточный ион, в котором атом азота находится в неактивном положении. Эти реакции также должны были бы идти через промежуточные соединения, для которых йн равны нулю. Оно включает член - рЛ / ь определяющий место атаки в соответствующем изосопряженном альтернантном углеводороде. Поскольку Nt для ос-положения нафталина ( 1 81) гораздо меньше, чем для, р-положения ( 2 12), атака происходит предпочтительно в а-положение. Такая же предпочтительность а-по-ложения сохраняется при переходе к хинолину и изохинолину. Поэтому замещение в р-положение может стать предпочтительным, только если последний член в уравнении (9.52) перевешивает это отличие. Очевидно, это не происходит, так как всегда более благоприятным является а-положение. [4]
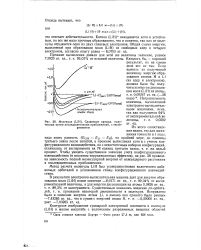 |
Молекула ( LiH. Сравнение кривых, полученных путем последовательных приближений, с экспериментом. [5] |
Метод расчета молекулы LiH был усовершенствован включением добавочных орбиталей и усложнением схемы конфигурационного взаимодействия. [6]
 |
Энергетическая диаграмма и графические изображения граничных молекулярных орбиталей акролеина. [7] |
Результаты расчета молекулы акролеина методом МОХ подробно обсуждены ранее. На рис. 19.5 показаны лишь уровни энергий его граничных орбиталей и их графические изображения. Ниже приводятся также собственные коэффициенты граничных орбиталей акролеина. [8]
При расчете молекул, содержащих гетероатомы ( галогены, О, N, S и др.), необходимо наряду с кулоновским ( а) и резонансным ( р) интегралами для атома углерода ( см. уравнения 16, 17) применять аналогичные интегралы для гетероато-мов. Обычно их выражают через соответствующие параметры для атома углерода, вводя для гетероатома Z необходимые поправочные коэффициенты hz и kcz, которые подбирают из опытных данных. Эти коэффициенты зависят от порядка связи гетероатома с атомом углерода ( например, в анилине N -, в пиридине N, в нитрилах N) и от валентного состояния гетероатома ( например, N в пиридинии); некоторые поправочные коэффициенты приведены ниже. [9]
При расчете молекулы по методу валентных структур исходят из собственных функций fA фв... Их определяют вариационным методом, находя минимальное значение энергии молекулы. Разность между истинной энергией молекулы и энергией наиболее устойчивой предельной структуры называют энергией резонанса. Эта величина не может быть найдена непосредственно из эксперимента, так как предельные структуры в действительности не существуют, но ее можно с некоторыми допущениями рассчитать на основании данных о теплотах гидрирования и горения. [10]
При расчете молекул, содержащих несколько атомов, решение векового уравнения позволяет найти энергетические уровни электронов, разности которых приблизительно определяют частоту электронного спектра. Число таких энергетических уровней сравнительно велико. Если учесть, что оптические переходы возможны не только между основным и возбужденными, но и между двумя возбужденными состояниями, можно ожидать появления большого числа спектральных линий. Например, в спектре бензола отмечается три линии вблизи частоты 3600 см-1: одна интенсивная и две слабые. Причина этого заключается в том, что далеко не между всеми энергетическими уровнями оптический переход разрешен. [11]
При расчете молекул по методу Хюккеля делается ряд дополнительных упрощающих предположений. [12]
При расчете молекулы по методу валентных структур исходят из собственных функций v фв... Их определяют вариационным методом, находя минимальное значение энергии молекулы. Разность между истинной энергией молекулы и энергией наиболее устойчивой предельной структуры называют энергией резонанса. Эта величина не может быть найдена непосредственно из эксперимента, так как предельные структуры в действительности не существуют, но ее можно с некоторыми допущениями рассчитать на основании данных о теплотах гидрирования и горения. [13]
Проведенные выше расчеты молекулы HF не претендуют на точность и преследуют лишь очень ограниченные цели. В качестве исходных данных были использованы потенциалы ионизации молекулы и изолированных атомов и в результате найдено электронное распределение в молекуле. Главная задача в такого рода расчетах должна состоять в том, чтобы получить максимум результатов с минимумом исходных данных. Это трудно осуществить, рассматривая ( как это было сделано выше) лишь изолированную молекулу вне связи с родственными ей соединениями. [14]
Для завершения расчета молекулы циклобутадиена нам остается только вычислить результирующую) волновую функцию основного состояния молекулы. [15]
Страницы: 1 2 3 4