Расчет - температурное напряжение
Cтраница 1
Расчет температурных напряжений производят следующими методами. [1]
Расчет температурных напряжений производится методом разбиения на интервалы во времени со смягчением в них начальных условий. [2]
Расчет температурных напряжений при пластических деформациях значительно труднее, чем для упругого тела. Исходные соотношения, связывающие напряжения и деформации, становятся нелинейными, вследствие чего необходимо решать нелинейные дифференциальные уравнения. Из-за нелинейности недопустимо наложение решений, поэтому нельзя, как это делалось для упругого тела, рассматривать отдельно задачу о напряжениях в теле от внешней нагрузки и задачу о чисто температурных напряжениях. [3]
Расчет температурных напряжений в упругой области ( для хрупких материалов, наиболее опасных с точки зрения их прочности), выполняемый методами термоупругости по известным температурным полям, не дает ответа на то, какие напряжения наиболее опасны, в каком случае произойдет разрушение и какой материал обладает лучшей или худшей сопротивляемостью действию температурных полей при различных условиях его реальной работы. Другими словами, теория термоупругости и наука о сопротивлении материалов в настоящее время не располагают критериями прочности в указанных выше условиях. Эти критерии необходимы для правильного выбора материалов и расчета соответствующих элементов конструкций. [4]
Расчет температурных напряжений при неустановившемся тепловом режиме представляет известные трудности из-за меняющихся во времени основных расчетных параметров. Напряжения при этом меняются от максимума до минимума в различных точках стенки изделия в связи с изменением температуры. Для определения характера кривой температурного перепада существует несколько методов. Наиболее простой метод - графический. Толщина стенки делится на несколько слоев, в которых строятся температурные кривые по граничным условиям. В качестве варианта расчета используют аналитическое решение по разности температур при нестационарном режиме [3] для случаев пластинок, цилиндров, шаров. [5]
Расчет температурных напряжений в роторах высокого и среднего давления производился по программе решения осесимметричной задачи теории упругости, разработанной Институтом проблем машиностроения АН - Украины на основе метода конечных элементов. Результаты расчета температурных напряжений в роторах при различных режимах работы турбины, а также напряжений от центробежных сил при номинальной частоте вращения приведены в табл. 5.5. Значения осевых напряжений ог даны без учета концентрации напряжений для наружной поверхности бочки ротора в сечении между рассматриваемой и следующей ступенями. Значения окружных напряжений о, относятся к расточке ротора под соответствующей ступенью. [6]
Для расчета температурных напряжений в диске необходимо иметь. [7]
Для расчета нестационарных температурных напряжений в трубопроводах можно применять ( после надлежащей апробации) и другие существующие или создаваемые методы и программы ( см., например, [13]), При построении их допустимо использование следующих упрощающих условий: отсутствует теплообмен с окружающей средой через теплоизоляцию; теплофизические характеристики материала ( коэффициент линейного расширения, удельная теплоемкость, коэффициент теплопроводности) и модуль упругости не изменяются по толщине стенки и принимаются в зависимости от ее средней температуры для данного момента времени. [8]
В задаче расчета температурных напряжений принято, что высота шпангоута невелика и не учитывается разность температуры и сил в сечении. Иногда с этим обстоятельством приходится считаться. Расчет кольца двутаврового поперечного сечения, соединенного с оболочкой, показывает, как влияет высота сечения и неравномерный нагрев на напряженное состояние. Температура обшивки наружного пояса шпангоута считается одинаковой и равной t0 - t, а температура стенки и внутреннего пояса равной нулю. [9]
Разработана методика расчета температурных напряжений в стыках труб из стали марки Х5М, выполненных аустенитными электродами, которая была подтверждена экспериментальными данными. [10]
Задача о расчете температурных напряжений в осессимметрично нагретых оболочках вращения существенно упрощается в двух часто встречающихся на практике случаях. [11]
Приведен вывод уравнений для расчета температурных напряжений в защитном тгрнопяастсгсм г силсгом несущей стенлопдастивовоы слоях. [12]
 |
Термо механическая поверхность материала. [13] |
Метод конечных разностей также может быть применен для расчета упругих температурных напряжений в элементах конструкций, но он обладает меньшей общностью по сравнению с рассмотренными. [14]
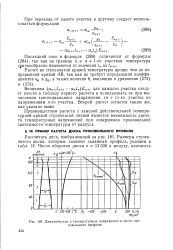 |
Динамические и температурные напряжения в диске произвольного профиля. [15] |
Страницы: 1 2 3