Расчет - температурное напряжение
Cтраница 2
Преимуществом расчета с заменой действительной температурной кривой ступенчатой линией является возможность расчета температурных напряжений при совершенно произвольной зависимости температуры от радиуса. [16]
По формуле (3.132) при Ре 24 888, Н 0 21 произведены расчеты безразмерных температурных напряжений ву для различных значений Bii и B z, результаты которых представлены в виде графиков на рис. 3.17, 3.18. Из графиков видно, что с ростом теплоотдачи с поверхностей вне области нагрева напряжения уменьшаются. [17]
Рассмотрим схему, позволяющую автоматизировать указанные выше операции и исключить участие оператора в процессе расчета температурных напряжений. Для этого в устройство ( рис. 97) вводится коммутационное поле КП с контактной сеткой. Обычный стол ЭГДА заменен вакуумным столом ВС, что позволяет создать идеальный контакт между моделью и контактной сеткой. [18]
Имеются специальные руководящие технические материалы по расчету трубопроводов с учетом нестационарных режимов [8, 10, 11], содержащие методики расчета температурных напряжений и указания по учету их при оценке прочности. [19]
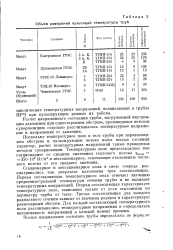 |
Объем измерений пульсаций температуры труб. [20] |
Поскольку температурное поле в теле трубы при неравномерном обогреве и пульсирующем потоке имеет весьма сложный характер, расчет температурных напряжений также проводился методом суперпозиции. ВОСПр 350 - 103 Вт / м2 и нестационарное, отвечающее отклонению теплового потока от его среднего значения. [21]
Оценку температурных напряжений в трубных решетках предусматривает и КОД ASME [39], где приведены упрощенные аналитические зависимости для расчета температурных напряжений, полученные из условия, что весь температурный перепад в трубной решетке сосредоточен в очень тонком поверхностном слое, жесткость которого пренебрежимо мала по сравнению с жесткостью самой решетки. Но даже для использования этих формул нужно знать температурный перепад по толщине трубной решетки. [22]
Другим примером, иллюстрирующим эффективность применения простых физических схем, отвечающих точности исходных, данных и требуемых практикой результатов, может служить статья Ю. А. Шиманского Расчет температурных напряжений и деформаций корпуса, опубликованная в двенадцатом номере журнала Судостроение за 1940 г., а затем в Сборнике статей по судостроению в 1954 г. Необходимость исследования этого вопроса возникла впервые в начале 30 - х годов во время перевозки нефтепродуктов из Баку в Астрахань. Температура жидкого груза в условиях перевозки может достигать порядка 100, что, как показала практика, влечет за собой расстройство заклепочных соединений корпуса и уменьшение его общей прочности. Не менее важным для обеспечения параллельности осей судовых приборов и устройств является учет ( при постройке корабля в процессе расточки оснований под различные устройства) ожидаемой при эксплуатации разности температур основных продольных связей корпуса. [23]
Расчетные формулы ( 17) и ( 18) для нормальных напряжений в стержне по своей структуре достаточно просты, затруднения могут возникнуть при определении главных осей и упруго-геометрических характеристик сечения, что будет разобрано в следующем разделе, а сейчас рассмотрим вкратце расчет температурных напряжений. [24]
Эти рассуждения п приведенный пример расчета являются сугубо схематичными и ориентировочными. Расчет температурных напряжений необходимо вести с учетом неупругих деформаций и особенно зависимости всех параметров от температуры. [25]
Для расчета температурных напряжений в цилиндрических деталях, соединенных встык, используют несколько моделей: тонкие диски равной толщины; бесконечно длинные цилиндры; тонкий диск и бесконечно длинный цилиндр; тонкие диски неодинаковой толщины с криволинейными торцами. [26]
Расчет температурных напряжений в роторах высокого и среднего давления производился по программе решения осесимметричной задачи теории упругости, разработанной Институтом проблем машиностроения АН - Украины на основе метода конечных элементов. Результаты расчета температурных напряжений в роторах при различных режимах работы турбины, а также напряжений от центробежных сил при номинальной частоте вращения приведены в табл. 5.5. Значения осевых напряжений ог даны без учета концентрации напряжений для наружной поверхности бочки ротора в сечении между рассматриваемой и следующей ступенями. Значения окружных напряжений о, относятся к расточке ротора под соответствующей ступенью. [27]
Напряжения, вызванные перепадом температуры по толщине стенки, на основании теории упругости в длинных цилиндрах при заданных свойствах материала ( коэффициенте удлинения р, модуле упругости Е, коэффициенте Пуассона v) зависят от абсолютного значения температурного перепада по толщине стенки At и характера распределения температур. Преобразование общих формул для расчета температурных напряжений с учетом параболического закона изменения температуры по толщине стенки в процессе пуска позволяет получить расчетные уравнения для определения напряжения в текущей точке стенки. [28]
Решение задачи с учетом расчета температурных напряжений цилиндрического сосуда в условиях неравномерного поля температур математически может быть сведено к решению некоторой краевой задачи, определяемой системой (6.49) восьми линейных дифференциальных уравнений первого порядка. Базовые неизвестные заданы в (6.48); зная их значения, можно найти все остальные величины, характеризующие напряженно - деформированное состояние в корпусе аппарата. [29]
Страницы: 1 2 3