Расчет - оболочка - вращение
Cтраница 2
В случае расчета оболочек вращения сложной формы дополнительно вводятся массивы T ( Nl: N2), PY ( JN1: N2) согласно указанному выше формату. [16]
Задача о расчете оболочек вращения наиболее просто решается в том случае, когда возможно принять, что напряжения, возникающие в оболочке, постоянны по толщине, и, следовательно, изгиб оболочки отсутствует. Теория оболочек, построенная в этом предположении, называется безмоментной теорией оболочек. [17]
Задача о расчете оболочек вращения наиболее просто решается в том случае, когда возможно принять, что напряжения, возникающие в оболочке, постоянны по толщине и, следовательно, изгиб оболочки отсутствует. Теория оболочек, построенная в этом предположении, называется безмоментной теорией оболочек. [18]
Задача о расчете оболочек вращения наиболее просто решается в том случае, когда можно принять, что напряжения, возникающие в оболочке, постоянны по толщине и, следовательно, изгиб оболочки отсутствует. Теория оболочек, построенная в этом предположении, называется безмоментной теорией оболочек. [19]
Задача о расчете оболочек вращения наиболее просто решается в том случае, когда возможно принять, что напряжения, возникающие в оболочке, постоянны но толщине, и, следовательно, изгиб оболочки отсутствует. Теория оболочек, построенная в этом предположении, называется безмоментной теорией оболочек. [20]
Статический и динамический расчеты геометрически нелинейных оболочек вращения. [21]
Сложнее обстояло с расчетом оболочек вращения на неосе-симметрнчные нагрузки. Наиболее важной из них является обрат-носимметричная нагрузка, иногда называемая также ветровой. Рейсснеру) преобразовывал дифференциальные уравнения в духе, типичном для цюрихской школы, стремясь получить решение в форме плохо сходящихся в данном случае гипергеометрических рядов, что ему и удалось. При этом были обнаружены две квадратуры, а также возможность комплексного преобразования, так что расчет сферической оболочки на ветровую нагрузку в итоге оказался сведенным к интегрированию одного уравнения второго порядка. Последний результат был обобщен затем в работе [126] для оболочек вращения произвольной формы. [22]
Основной интерес при расчете оболочек вращения представляют случаи k 0 и k 1, называемые соответственно осесимметричным ( симметричным) и обратносимметричным. [23]
В разработке упрощенных методов расчета оболочек вращения иа осесимметричную нагрузку особенно велики заслуги И. Я. Штаермана [221], И. [24]
Теперь рассмотрим несколько примеров расчета симметрично нагруженных оболочек вращения по безмоментной теории. [25]
Применение этого метода при расчете оболочек вращения требует формулировки краевой задачи на основе дифференциальных уравнений первого порядка. Система уравнений моментной теории оболочек вращения приведена в гл. [26]
В большинстве случаев при расчете оболочек вращения их края рассматривают свободными и расчет производят с достаточной для практики точностью по формулам безмоментной теории расчета. В действительности край оболочки вращения обычно нагружен равномерно распределенными краевой силой и краевым радиальным моментом. Краевые сила и момент появляются вследствие ограничения свободы деформации края оболочки. [27]
В большинстве случаев при расчете оболочек вращения их края рассматривают свободными и расчет производят с достаточной для практики точностью по формулам безмоментноп теории расчета. В действительности край оболочки вращения обычно нагружен равномерно распределенными краевой силой и краевым радиальным моментом. Краевые сила и момент появляются вследствие ограничения свободы деформации края оболочки. [28]
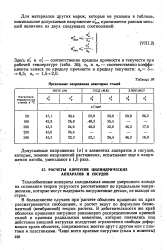 |
Предельные напряжения некоторых сталей. [29] |
В большинстве случаев при расчете оболочек вращения их края рассматриваются свободными, и расчет ведут по формулам безмо-ментной ( мембранной) теории расчета. В действительности же край оболочки вращения натружен равномерно распределенными краевой силой и краевым радиальным моментом, которые появились под действием внешней нагрузки вследствие ограничения свободы деформации краев оболочек, сопряженных жестко друг с другом или с плитами и пластинками. [30]
Страницы: 1 2 3 4