Расчет - электронная плотность
Cтраница 3
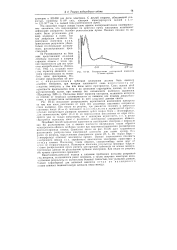
Последние, таким образом, сколько-нибудь четко друг от друга не отграничиваются. Пунктиром показаны результаты проверки теоретического распределения путем расчета электронной плотности на основе экспериментальных данных по рассеиванию аргоном электронов. Как видно из рисунка, обе кривые практически совпадают. [31]
Мы обсудим псевдопотенциальный подход Андерсона, так как он может быть интерпретирован в рамках использованной в этой статье теории. Так, в отличие от Андерсона мы рассматриваем его подход как попытку расчета электронной плотности в молекуле р ( г) при помощи одночастичного потенциала F ( r) метода функционала плотности. [32]
Правильное определение знаков амплитуд для большинства отражений на самой ранней стадии позволяет резко сократить процедуру расчета электронной плотности и даже свести задачу к одному единственному построению распределения. [33]
Метод проб и ошибок состоит в следующем: из тех или иных данных делается предположение о положении атомов. Затем рассчитывают значения / &, ) Наблюдаемые интенсивности сравнивают с расчетными. Если они согласуются достаточно хорошо, их можно использовать для расчета электронной плотности. Составленная карта электронной плотности будет иметь Максимумы, положения которых немного отличаются от первоначально предполагаемых. Затем положение атомов несколько меняют и рассчитывают другой набор F ( h h i), который берут для расчета новых значений электронной плотности по новому синтезу Фурье. Фурье-представление прекрасно изображало бы структуру кристалла в том случае, если бы можно было с большой точностью определить все коэффициенты и фазовые константы и если бы можно было использовать бесконечно большой набор рефлексов. На практике это не так и используется лишь конечное число членов ряда, что задается экспериментальными условиями и используемой длиной волны. Успех определяется тем, близки ли предполагаемые положения атомов в каких-то точках к истинным положениям, что определяется мерой согласованности расчетных и наблюдаемых интенсивностей. Если они близки, правильные положения могут быть найдены путем небольших разумных смещений некоторых или всех атомов из Первоначальных положений. Применимость такого прямого приближения резко уменьшается при увеличении размеров и сложности молекулы органического соединения. [34]
Черджвин и Коул-сон [3] показали, что если в молекуле углеводорода с сопряженными связями все интегралы перекрывания Srs и все резонансные интегралы p % g между соседними атомами одинаковы для всех связей ( обозначим их соответственно 5 и 3), то электронная плотность и порядки связей, вычисленные по уравнениям ( 330) и ( 331), совпадают со значениями, полученными в результате расчетов, в которых перекрывание принималось равным нулю. Этот вывод очень важен, так как из него следует, что расчеты электронной плотности и порядков связей, выполненные простым методом МО ( при пренебрежении перекрыванием), оказываются справедливыми и при внесении поправки на перекрывание. Однако указанный вывод неприменим к молекулам с гетероатомами, поскольку в такой системе не все кулоновские интегралы равны между собой. Тем не менее числовые значения, полученные Чердж-вином и Коулсоном, показывают, что даже в этом случае учет перекрывания приводит к незначительным изменениям в величинах порядков связей. [35]
Дополнением к основной машине X-RAC служат две самостоятельные установки S-РАС и R-РАС. Машина, следовательно, может применяться с удобством и для расчета структурных амплитуд. R - РАС является устройством памяти. Наличие такого устройства позволяет объединять расчеты электронной плотности и структурных амплитуд в непрерывные циклы и делает машину Пепинского почти столь же гибкой, как и универсальные вычислительные машины. Она может решать разнообразные структурные задачи начиная от суммирования рядов и кончая минимализаиией межатомной функции ( см. ниже, стр. [36]
В основу работы Хаша был положен расчет по теории абсолютных скоростей реакций. Поскольку реакции разряда Хаш считал всегда протекающими адиабатическим образом ( в квантовомеханическом смысле), то, естественно, он не пользовался принципом Франка - Кондона и трансмиссионный коэффициент полагал равным единице. Как показал Хаш, для электрохимической кинетики очень важную роль играет конкретное распределение плотности электронного заряда в активированном состоянии. Этот результат является малообнадеживающим, поскольку в настоящее время не существует методов расчета электронной плотности в таких сложных системах, как активированные ионы, окруженные дипольной гидратной оболочкой. Именно по этой причине в интересных с принципиальной стороны работах Геришера [3], в которых рассматривались гетерогенные реакции типа II, не удалось получить конкретных количественных результатов, допускающих сравнение с опытом. Изучая окислительно-восстановительные реакции, протекающие на металлическом и полупроводниковом электродах, Геришер считал, что энергия активации, связанная с франк-кондоновским барьером, главным образом обусловлена смещением атомов, находящихся в первой координационной сфере иона. Хотя это представление правильно передает физическую картину, оно не привело к количественным результатам. [37]
В некоторых я-электронных системах вклад ст-составляющей пренебрежимо мал по сравнению с вкладом я-составляющей. Дипольный момент а-составляющей можно представить в виде суммы дипольных моментов отдельных 0-связей, для которых в литературе имеются табулированные значения. При этом не следует забывать о вкладах несвязывающих атомных орбита-лей - неподеленных электронных пар ( например, на атоме азота в пиридине или на атоме кислорода в карбонильных соединениях), которые имеют большее значение, чем дипольные моменты а-связей. Известно, что подстановка плотности я-элек-тронов, найденной методами МОХ или ССП, в выражение для дипольного момента приводит к завышенным значениям. Правильные значения ц получаются, если для расчета электронных плотностей используется метод, в котором значения а ( или ас) зависят от зарядов в соответствующих положениях. Хорошие результаты дают также методы, в которых явно учитываются 0-электроны. Однако в таком случае простое выражение (11.64) должно быть заменено более сложным. [38]
В некоторых я-электронных системах вклад а-составляющей пренебрежимо мал по сравнению с вкладом я-составляющей. Дипольный момент а-составляющей можно представить в виде суммы дипольных моментов отдельных 0-связей, для которых в литературе имеются табулированные значения. При этом не следует забывать о вкладах несвязывающих атомных орбита-лей - неподеленных электронных пар ( например, на атоме азота в пиридине или на атоме кислорода в карбонильных соединениях), которые имеют большее значение, чем дипольные моменты а-связей. Известно, что подстановка плотности я-элек-тронов, найденной методами МОХ или ССП, в выражение для дипольного момента приводит к завышенным значениям. Правильные значения ji получаются, если для расчета электронных плотностей используется метод, в котором значения а ( или ас) зависят от зарядов в соответствующих положениях. Хорошие результаты дают также методы, в которых явно учитываются ст-электроны. Однако в таком случае простое выражение (11.64) должно быть заменено более сложным. [39]
 |
Распределение электронной плотности в атоме аргона. [40] |
Подобный способ выражения вероятности нахождения электрона с помощью как бы размазывания его и оценки плотности получаемого таким образом однородного электронного облака особенно удобен при волновомеханическом рассмотрении многоэлектронных атомов. Сплошная линия на рис. 111 - 30 дает теоретически рассчитанное распределение электронной плотности для атома аргона. Как видно из рисунка, определенным электронным слоям ( К, Ь, М)) теории Бора - Зоммерфельда отвечают максимумы кривой. Последние, таким образом, сколько-нибудь четко друг от друга не отграничиваются. Пунктиром показаны результаты проверки теоретического распределения путем расчета электронной плотности на основе экспериментальных данных по рассеиванию аргоном рентгеновских лучей. Хотя первый минимум на пунктирной кривой и не выявлен, однако общий ее характер хорошо согласуется с требованиями теории, тем самым подтверждая последнюю. [41]
Подобный способ выражения вероятности нахождения электрона с помощью как бы размазывания его и оценки плотности получаемого таким образом электронного облака особенно удобен при квантовомеханнческом рассмотрении многоэлектронных атомов. Сплошная линия на рис. 111 - 26 даст теоретически рассчитанное распределение электронной плотности для атома аргона. Как видно из рисунка, определенным электронным слоем ( К, L, M) теории Бора - Зоммерфельда отвечают максимумы кривой. Последние, таким образом, сколько-нибудь четко друг от друга не отграничиваются. Пунктиром показаны результаты проверки теоретического распределения путем расчета электронной плотности на основе экспериментальных данных по рассеиванию аргоном электронов. Как видно из рисунка, обе кривые практически совпадают. [43]
Ошибки при использовании изоморфных производных, полученных путем замены иона металла, находящегося в нативном белке, на более тяжелые элементы, могут возникать из-за изменений в структуре металл-лигандных центров при замене металла. Кристаллографические исследования карбоксипептидазы А [29, 67], карбоангидразы С [68, 69] и нуклеазы стафилококка [33] показали, что более тяжелый ион металла смещен относительно металла в нативном белке, как и следовало ожидать, исходя из различных координационных свойств и ионных радиусов соответствующих металлов. Из-за вполне вероятного в этих условиях изменения конфигурации боковых цепей аминокислот, являющихся лигандами, отсутствие точного изоморфизма приводит к некоторой ошибке в расчете фаз. Эти изменения также могут привести к утрате точного изоморфизма. Вообще говоря, эта проблема может быть частично решена путем использования фаз, полученных для нескольких изоморфных производных. При расчете электронной плотности вблизи центра связывания металла для производного, в котором тяжелый атом замещает катион нативного белка, могут быть использованы фазы, определенные для других производных. [44]
Необходимо еще раз отметить что любая попытка использования имеющихся расчетов электронной плотности молекулы пурина для предсказания химических реакций должна быть сделана с большой осторожностью. Наличие различных функциональных групп, естественно, изменяет распределение электронов в молекуле. Такого типа сведения представляют для химика органика не больше чем академический интерес, так как мочевая кислота существует исключительно в кето-форме и до сих пор не известно замещение оксигрупп электрофиль-ными или нуклеофильными реагентами. Можно надеяться, что будут предприняты расчеты таких реакционноспособных молекул, как 2 6 8-трихлорпурин, и химики смогут экспериментально проверить полученные результаты. Вполне возможно, что в будущем расчеты электронной плотности азотсодержащих гетероциклических систем удастся экспериментально проверить, коррелируя данные магнитного резонанса на ядрах 13С с величинами электронной плотности на атомах углерода. Такие надежные данные могут иметь большое значение при изучении химической реакционной способности соединений. [45]
Страницы: 1 2 3 4