Расчет - колебательная система
Cтраница 2
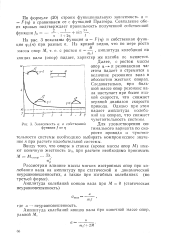 |
Зависимость а и собственной функции f от г. [16] |
Для удовлетворения оптимального варианта по скорости привода и чувствительности системы необходимо выбирать компромиссное значение п при расчете колебательной системы. [17]
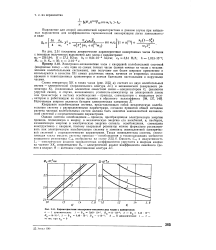 |
Характеристики электронно-механических часов с камертоном. [18] |
Кварцевая колебательная система, представляющая собой механическую колебательную систему с распределенными параметрами, согласно принятой общей методике расчета часовых колебательных систем должна быть заменена эквивалентной механической системой с сосредоточенными параметрами. [19]
В книге дан обзор известных методов статистической динамики, обоснованы вариационные методы исследования, приведены прикладные задачи и инженерные методы расчета дискретных колебательных систем, и также статические и динамические задачи для упругих конструкций ( балок, пластин, оболочек), вопросы распространения волн в стохастически неоднородных средах. [20]
Если колебательная система конструируется из двухпроводных линий, то поперечные размеры рассчитываются из тех же соображений, что и при расчете колебательных систем на коаксиальных линиях. [21]
При использовании ламп с дисковыми или цилиндрическими выводами, непосредственно сочленяющимися с контурами в виде отрезков длинных линий, даже в диапазоне дециметровых волн оказывается возможным не учитывать влияние индуктивностей выводов и производить расчеты колебательных систем по формулам двухконтурных автогенераторов. [22]
Приводы ( вибровозбудители) вибрационных конвейеров по роду двигательной энергии бывают электромагнитные, электромеханические ( центробежные и эксцентриковые), гидравлические и пневматические. Следует отметить, что при сравнительной простоте конструкций, вибрационные конвейеры требуют более тщательного и квалифицированного расчета колебательной системы, правильности выбора параметров и вы-сококачественности изготовления. Недооценка этих условий приводит к недостаточно эффективным, а в ряде случаев даже к отрицательным результатам. [23]
На основании сравнения программ по разным критериям эффективности показано, что процедура Кутта-Мерсона ( см. [324]) имеет оптимальные характеристики при расчете колебательных систем. Поэтому было проведено сравнение с программой, реализующей метод Кутта-Мерсона. Критерием сравнения являлось время, необходимое для расчета траектории при сохранении аддитивных интегралов движения в пределах заданной точности. Сравнения показали, что при расчетах траекторий трехатомных молекул и небольших траекторий пятиатомных молекул без существенного разброса характеристических времен программы обладают сравнимым быстродействием. Так, для расчета траектории движения молекулы N2O на временах порядка 50 колебаний молекулы этим программам требуется около 20 с машинного времени ЭВМ БЭСМ-6, для расчета молекулы CHF3 примерно на таком же числе колебаний - порядка 3 мин, а для расчета траектории совместно с оператором производных по начальным условиям - 8 - 12 мин. [24]
 |
Схемы машин для испытаний образцов изгибом при вращении. [25] |
Колебания рассматриваемой системы возбуждаются статическим биением образца, зависящим от точности изготовления образца, захвата и его опор. Анализ сводится к расчету одномассной колебательной системы с возмущением колебаний путем гармонического перемещения свободного конца образца. Если нагружение рычага 7 ( см. рис. 1, б) происходит через пружину, в динамической схеме необходимо учесть приведенную жесткость с2 ( рис. 6, б) механизма нагружения и внешнее и внутреннее трение k2 в элементах соединения механизма нагружения. Если силовая схема машины содержит демпфер, сочлененный с рычагом 7 ( см. рис. 1 6), то R2 - неупругое сопротивление демпфера. [26]
 |
Схемы машин для испытаний образцов изгибом при вращении. [27] |
На рис. 6, а mi - масса, приведенная к свободному концу испытуемого образца с перемещением х; Ci - жесткость испытуемого образца; ki - неупругое сопротивление материала образца и трение в соединитель-нах элементах. Колебания рассматриваемой системы возбуждаются статическим биением образца, зависящим от точности изготовления образца, захвата и его опор. Анализ сводится к расчету одномассной колебательной системы с возмущением колебаний путем гармонического перемещения свйбодного конца образца. Если нагружение рычага 7 ( см. рис. 1, б) происходит через пружину, в динамической схеме необходимо учесть приведенную жесткость С2 ( рис. 6, б) механизма нагружения и внешнее и внутреннее трение 2 в элементах соединения механизма нагружения. Если силовая схема машины содержит демпфер, сочлененный с рычагом 7 ( см. рис. 1, б), то i. Во время работы машины захвати участвует в колебательном движении, описывая некоторую замкнутую кривую в плоскости, перпендикулярной оси образца. [28]
Расчет автогенераторов распадается на две части: расчет режима работы лампы и расчет колебательной системы. Расчет режима позволяет определить напряжения на аноде, сетке, а следовательно, требуемый коэффициент обратной связи, а также величину сопротивления нагрузки. Эти параметры вместе с заданной частотой берутся за основу при расчете колебательной системы. В табл. 3 - 2 приведена сводка расчетных ф-л для определения параметров колебательных систем двухконтурных автогенераторов. При этом принято, что емкости контуров образуются междуэлектродными емкостями лампы или предварительно выбранными емкостями конденсаторов настройки. [29]
Расчет автогенераторов распадается на две части: расчет режима работы лампы и расчет колебательной системы. Расчет режима позволяет определить напряжения на аноде, сетке, а следовательно, требуемый коэффициент обратной связи, а также величину сопротивления нагрузки. Эти параметры вместе с заданной частотой берутся за основу при расчете колебательной системы. В табл. 12 - 2 приведена сводка расчетных формул для определения параметров колебательных систем двухконтурных автогенераторов. При этом принято, что емкости контуров образуются междуэлектродными емкостями лампы или этими емкостями и выбранными предварительно емкостями конденсаторов настройки. [30]
Страницы: 1 2 3