Расчет - скорость - рост
Cтраница 1
 |
Параметры диффузии углерода в титане. [1] |
Расчет скорости роста карбидных слоев при насыщении титана углеродом. [2]
Расчет скоростей роста кристалла, несомненно, выходит за рамки равновесной статистической механики. Такие расчеты ведутся на основе либо теории переноса, либо кинетической теории, либо же статистической механики неравновесных процессов. [3]
При расчете скорости роста был принят первый порядок по концентрации углеводорода, а концентрацию углеводорода находили, как и в опытах с ацетиленом, по количеству образовавшейся сажи в предположении, что при этом процессе никакие газообразные углерод-содержащие продукты не образуются. [4]
Бест [230] произвел расчеты скорости роста капельки для температуры воздуха 273 К и давления 900 мб. Он получил, что при конденсации водяного пара на сравнительно больших ядрах рост капелек радиусом от 0 75 до 1 - 2 мкм происходит весьма быстро, за доли секунды. В этих пределах капельки являются достаточно концентрированными растворами, что и является причиной понижения равновесной упругости пара и интенсивной конденсации водяного пара. Но при дальнейшем росте концентрация раствора играет малую роль. Для ядер конденсации с массой 10 - 15 кг время роста капелек до радиуса 15 мкм составляет почти 50 мин. Следовательно, в быстро развивающихся конвективных облаках образование облачных капелек радиусом более 10 мкм нельзя объяснить конденсацией водяного пара. Расчеты показали, что электрические силы могут влиять на скорость конденсационного роста капелек радиусом не более 1 мкм. [5]
Получена формула для расчета скорости роста эпитаксиальных слоев GaAs в систе - Ga - AsGlj - Н2 с помощью решения уравнения непрерывности с учетом диффузии тазовых компонентов через пограничный слой. Наблюдается согласие между экспериментальными скоростями роста эпитаксиальных слоев GaAs и вычисленными по предложенной формуле. [6]
В U-3 ] выполнены расчеты скоростей роста итравлениякремнил в хлоридной системе, из которых следует, что скорость процесса в проточной системе пропорциональна диффузионному потоку молекул крем-нийсодержащего соединения через пограничный слой. [7]
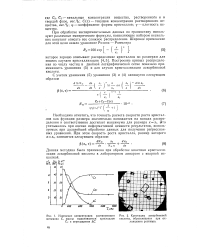 |
Изменение концентрации растворенного [ IMAGE ] Кристаллы аскорбиновой витамина С, массы выделившихся кристаллов кислоты, образующиеся при ох - Ст и пересыщения ДС. лаждении раствора. [8] |
Необходимо отметить, что точность расчета скорости роста кристаллов как функции размера значительно понижается на концах распределения и соответственно достигает максимума для размера х хе. [9]
Экспериментальные подтверждения применимости выражения ( 105) для расчета скорости роста гранул при обезвоживании растворов в кипящем слое и применявшиеся для этой цели методики приведены ниже. [10]
Из предыдущих рассуждений можно сделать вывод, что вся теоретическая основа для расчетов скоростей роста, разработанная Фольмером, Беккером, Дерингом и другими, должна быть отвергнута. [11]
То) / ( 7 / Т0) подразумевают соответственно поправки в расчете скорости роста трещины на влияние формы цикла нагружения, длительности выдержки под нагрузкой при максимальном ее уровне и температуре окружающей среды. Необходимо еще отметить, что суммирование поправок на условия нагружения при рассмотрении роли длительности цикла нагружения на развитие усталостных трещин в металлах (7.2) получено из энергетического анализа роли каждого из рассматриваемых параметров воздействия отдельно друг от друга без учета взаимного влияния указанных факторов. В случае рассмотрения влияния факторов друг на друга, что соответствует принципам синергетики, следует учесть еще эффект, когда в условиях многопараметрического воздействия можно выделить параметр порядка и через него выражать влияние всех факторов воздействия на эволюцию открытой системы. Сделанное замечание необходимо включить в рассмотрение для выявления границ взаимно независимого воздействия параметров нагружения на развитие усталостной трещины. [12]
Для большинства веществ уравнение ( 7) нельзя использовать в настоящем виде для расчета скоростей роста кристаллов, так как величина AG неизвестна. [13]
В приложении 2 к ОСТ 16.0.682.007 - 73 дана методика определения коэффициентов уравнений для расчета скорости роста дефектности изоляции. Существенным недостатком ОСТ является то, что при определении этих коэффициентов для межвитковой изоляции не учитываются в полной мере взаимодействие изоляции обмоточных проводов и пропитывающего состава, влияние микротрещин, возникающих в пленке пропиточного состава при старении и прорастающих через эмалевую пленку, залечиваемость пропиточным составом дефектов проводов и некоторые другие явления. [14]
Хотя сведения о росте нитрифицирующих бактерий и фитопланктона в природных условиях ограничены, на основании расчета специфических скоростей роста как функции концентрации азота аммония можно предположить конкуренцию одного над другим. [15]
Страницы: 1 2 3