Расчет - статистическая сумма
Cтраница 2
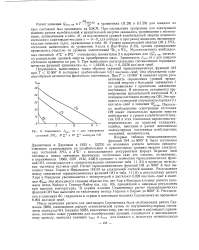 |
Зависимость / тах от v для электронных состояний Z2n., А. 2 и В2 2 молекулы ОН. [16] |
После окончания расчета для настоящего Справочника была опубликована работа Бау-манна [688], посвященная расчету статистической суммы по внутримолекулярным состояниям молекулы ОН. [17]
 |
Внутренняя энергия U ( p T для плазмы никеля ( обозначения, как на 1. [18] |
Принципиально присущая химической модели неопределенность с ограничением числа возбужденных состояний, используемых при расчете статистических сумм Qi ( T), мала и не сказывается на суммарных термодинамических функциях. [19]
Как следует из (2.22), для определения s - фактора бимолекулярных реакций следует провести расчеты статистических сумм исходных частиц и активированного комплекса. Расчет статистических сумм опирается на информацию о структурных и механических свойствах ( геометрия, моменты инерции, частоты нормальных колебаний и др.) молекул названных веществ. [20]
Наиболее удобным является использование функции потенциальной энергии лишь при определении конфигурации переходного состояния для расчета статистической суммы состояния, необходимой для статистического нахождения скорости при использовании специально подобранной величины коэффициента прохождения. [21]
Запишем выражения, определяющие энергетический спектр некоторых простейших систем; эти выражения понадобятся далее при расчетах статистических сумм молекул. [22]
Для вычисления Iff оба эти пути неприменимы, поскольку теплоемкость активированных комплексов измерить нельзя, а расчет статистических сумм требует знания уравнения потенциальной поверхности. [23]
Для вычисления Ef оба эти пути неприменимы, поскольку теплоемкость активированных комплексов измерить нельзя, а расчет статистических сумм требует знания уравнения потенциальной поверхности. [24]
Задача определения наблюдаемых термодинамических свойств веществ через микроскопические свойства атомов сводится, как известно из статистической физики, к расчету статистической суммы по состояниям. Аппарат статистических сумм позволяет определить микроскопические аналоги термодинамических функций, дает молекулярное обоснование законам термодинамики. Однако конкретное вычисление сумм по состояниям, и следовательно уравнения состояния, возможно только в предельных случаях - идеального газа и идеального гармонического кристалла. Аналитический расчет уравнений состояния сильно неидеального газа, жидкостей в настоящее время остается актуальной проблемой статистической теории. [25]
Хотя в формуле ( 52) множитель e - E / R T не содержится явно, он появляется при расчете статистических сумм, что связано с различием энергий основных состояний активированного комплекса и реагентов. Пусть qi - отнесенная к единице объема статистическая сумма ( для вещества г), из которой удален множитель, в котором фигурирует энергия основного состояния, а ф - соответствующая величина для комплекса без степени свободы, отвечающей координате реакции. [26]
В качестве нового и интересного результата можно рассматривать вывод о том, что в более точных теориях вместо энергетических уровней уравнения Шредингера при расчете статистической суммы и химического потенциала связанных пар надо использовать уровни энергии, находимые из уравнения Бете - Солпитера. [27]
Разумеется, малость величин сумм по состояниям вращательного и колебательного движений по сравнению с поступательными суммами не исключает необходимости их учета, поскольку все эти величины перемножаются при расчете статистических сумм для всех степеней свободы. [28]
Время жизни молекулы в отталкивательном состоянии практически равно времени взаимодействия атомов при столкновении; у молекул в отталкивательных состояниях отсутствуют дискретные уровни энергии и эти состояния не рассматриваются при расчетах статистических сумм. [29]
В связи с тем, что в третьей главе используются некоторые формулы статистической физики, в виде приложения к курсу дается изложение понятия о статистических суммах и вывод некоторых простейших формул для расчета статистических сумм. [30]
Страницы: 1 2 3 4