Значение - матрица
Cтраница 1
Значение матрицы S отражают относительные степени важности признаков У. [1]
Значение матрицы перехода за один шаг позволяет проследить изменение состояний системы через любое число шагов. Введем матрицу переходов за k шагов, каждый элемент которой представляет вероятность перехода из состояния i в состояние / за k шагов. Подчеркнем еще раз, что вероятности перехода - условные вероятности, которые описывают механизм смены состояний, но не могут полностью описать состояние системы. [2]
Значение матрицы S отражают относительные степени важности признаков У. [3]
Я 1-собственные значения матрицы g; ( g) - произвольная функция на G, постоянная на каждом классе сопряженных элементов. [4]
Подставляя значение матрицы предкомпенсатора в уравнение Р - формы, убеждаемся в выполнении декомпозиции многомерной ХТС на отдельные каналы регулирования. [5]
Определяем значения матриц, через которые выражаются коэффициенты уравнения состояния А. [6]
Этим определяется значение матрицы плотности. [7]
Пусть теперь значение матрицы точности R неизвестно. [8]
Первый оператор вводит значения матриц А и В по строкам, а также значения вектора С. Второй оператор выводит на печать элементы матриц А и - В. [9]
Первый оператор вводит значения матриц А, В по строкам, а также значения вектора С. Второй оператор выводит на печать элементы матриц А и В парами и по столбцам и в конце вывода каждого из столбцов печатает соответствующий элемент вектора С. [10]
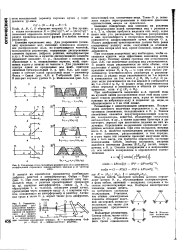 |
Различные типы связанных резонаторов ( I и зависимость коэффициента отражения эквивалентного зеркала р от частоты. [11] |
Модули собств, значений матрицы Джонса определяют потери О. [12]
В табл. 4.3 приведены значения матрицы усиления F ( t) при тех же значениях t и том же шаге. [13]
Квадраты наибольшего и наименьшего значений матрицы совпадают с наибольшим и наименьшим собственными числами эрмитовой матрицы А А. [14]
Расхождения между этими двумя значениями матрицы А вызваны ошибками округления. Уже этот простой пример матрицы третьего порядка показывает, как быстро накапливаются ошибки округления. При матрицах более высокого порядка это накопление ошибок округления может оказаться весьма серьезным. [15]
Страницы: 1 2 3 4