Расчет - энергия - решетка
Cтраница 3
Большой интерес представляют методы сравнительного расчета термодинамических функций и различных свойств веществ, развитые в основном в советской литературе. В 1932 г. [22] была показана возможность характеристики химических свойств элементов по разности тепловых эффектов образования хлоридов и оксидов и расчета энергий решеток оксидов из энергий решеток хлоридов. [31]
Авогадро, М - константа Маделунга ( эта константа характеризует геометрию решетки), - - хе - заряд катиона, е - заряд иона фтора и а - некоторая величина ( обычно равная И)), которая отражает межионные отталкивания. Be личину ДЯх можно определить по разности, если известны другие величины. Однако точность расчетов энергии решетки зависит от принятых приближенных значений радиуса катиона и предположения об определенном типе решетки. Поэтому точный расчет АЯг часто оказывается невозможным. [32]
Эта гипотеза очень привлекательна, так как она могла бы пролить свет на закономерности формирования поверхности бинарных систем и дать возможность предвидеть их свойства. Однако пока данных для расчета энергии решетки совершенно недостаточно и, кроме того, имеется ряд противоречивых фактов. [33]
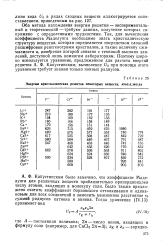 |
Энергии кристаллических решеток некоторых веществ, ккал / моль. [34] |
Оба метода нахождения энергии решетки - экспериментальный и теоретический - требуют данных, получение которых сопряжено с определенными трудностями. Так, для вычисления коэффициента Маделунга необходимо знать кристаллическую структуру вещества, которая определяется посредством сложной расшифровки рентгенограмм кристаллов, а также величину сжимаемости х, измерение которой связано с техникой высоких давлений, доступной лишь немногим лабораториям. Поэтому широко попользуется уравнение, предложенное для расчета энергий решеток А. Ф. Капустинским; вычисление U0 при помощи этого уравнения требует знания только ионных радиусов. [35]
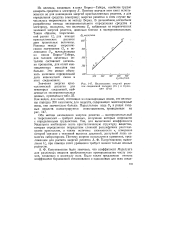 |
Взаимосвязь энергий решеток соединений кальция ( Ui и стронция ( / ц. [36] |
Оба метода нахождения энергии решетки - экспериментальный и теоретический - требуют данных, получение которых сопряжено с определенными трудностями. Так, для вычисления коэффициента Маделунга необходимо знать кристаллическую структуру вещества, которая определяется посредством сложной расшифровки рентгенограмм кристаллов, а также величину сжимаемости х, измерение которой связано с техникой высоких давлений, доступной лишь немногим лабораториям. Поэтому широко используется уравнение, предложенное для расчета энергий решеток А. Ф. Капустинским; вычисление t / 0 при помощи этого уравнения требует знания только ионных радиусов. [37]
В кристаллическом состоянии изучены все эти элементы, кроме радона. Особенность гелия заключается в том, что в твердое состояние он переходит только под давлением не ниже 25 атм. Преобладание структур с КПУ не соответствует результатам расчетов энергий решеток, согласно которым более предпочтительной должна быть ГПУ. [38]
Если определить UL из цикла Борна - Габера ( разд. Эти величины не всегда совпадают с радиусами, полученными в приближении сферического аниона ( величины в скобках), их называют термохимическими радиусами, чтобы отличить от ионных радиусов. Эти величины очень удобно использовать в качестве параметров при расчете энергии решетки. [39]
Ферсмана является постановка проблемы о вычислении энергии кристалла по двум инкрементам, свойственным катиону и аниону. Им же была дана только что описанная попытка ее решения. Простое суммирование эк ов может рассматриваться, конечно, только как первое приближение расчета энергии решетки. Сама система, по существу, является неправильной, так как она находится в противоречии с очевидным фактом неаддитивности ионных связей. [40]
Резюмируя три последних параграфа, можно оказать, что формула Варна дает самое точное выражение для расчета энергии решетки ряда бинарных соединений, но пользование ею возможно только после установления типа структуры и вычисления коэффициентов Маделунга для каждого типа. Первая формула Капустинокого позволяет вычислить энергию решетки любого соединения состава АтВ без предварительного знания их структуры, но с меньшей точностью. Значительно большую точность дает вторая формула Капустинокого. [41]
Уже из определения энергии решетки следует, что она представляет собой меру стабильности структуры. Если вещество встречается в двух модификациях, как, например, ромбическая и моноклинная сера, то самой стабильной будет та структура, которая обладает наибольшей энергией решетки. Энергия решетки тесно связана и с другими свойствами, например со сжимаемостью, с тепловым расширением, с температурами плавления и кипения, с твердостью и с прочими механическими свойствами кристаллов. При расчете энергии решетки различных кристаллов следует учитывать природу различных сил связи и классифицировать кристаллы по характеру сил связи. [42]
Из-за сферической формы атомов инертных газов можно ожидать, что в твердом состоянии последние будут иметь структуру плотнейшей упаковки; это действительно было обнаружено. Гелий образует плотнейшую гексагональную упаковку, а остальные инертные газы - плотнейшую кубическую упаковку. Чтобы объяснить этот факт, было выполнено большое число теоретических расчетов относительной устойчивости ПКУ и ПГУ. Один из методов расчета предполагает суммирование парных взаимодействий ближайших соседей. Это приближение аналогично тому, которое делают при расчете энергии решетки для ионных кристаллов. В последнем случае определяют взаимодействие одного катиона с одним анионом и затем умножают на геометрический множитель, называемый константой Маделунга. Применив этот метод для кристаллов инертных газов, получили, что ПГУ значительно более стабильна. Однако это находится в противоречии с экспериментальными данными. Более того, нельзя объяснить, исходя из парного взаимодействия сферически симметричных частиц, преобладание ПКУ у инертных газов. Поэтому были предложены два других метода расчета. В первом из них, предложенном Катбертом и Линнетом [2], допускают, что распределение заряда не является сферически симметричным. [43]
Энергию решетки металлических кристаллов нельзя точно рассчитать такими простыми способами, применяемыми для расчетов энергии решетки кристаллов с чисто ионной или ван-дер-ваальсовской связью. Для металлов подобный расчет возможен только на основе квантовой механики. Приближенный метод расчета был предложен Габером. Допускается также, что заряженные частицы обоих знаков расположены в виде упорядоченной решетки. Хотя эта модель неправильно отображает структуру металла и специфические металлические свойства, так как электроны в действительности двигаются свободно и не могут локализоваться в узлах решетки, она все же дает разумное приближение при расчете энергии решетки. [44]
Силы отталкивания возникают вследствие взаимного проникновения электронных облаков атомов. Это явление ( вместе с запретом Паули) препятствует слишком сильному сближению атомов. Попытки выразить в математической форме возникающие силы отталкивания встречают чрезвычайно большие трудности. Эти силы быстро возрастают с уменьшением расстояния между атомами, но закономерность, которой они подчиняются, имеет сложный характер. При расчетах энергий решеток ионных кристаллов галоидных солей щелочных металлов и окислов щелочноземельных металлов хорошие результаты были получены при применении предложенного Борном и Май-ером [14] простого выражения, описывающего зависимость потенциальной энергии от сил отталкивания. [45]
Страницы: 1 2 3