Расширение - кристалл
Cтраница 1
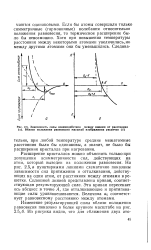 |
Зависимость силы взаимодействия между ионами от расстояния ( а. Вблизи положения равновесия масштаб изображения увеличен ( б. [1] |
Расширение кристаллов можно объяснить только при допущении асимметричности сил, действующих на атом, который выведен из положения равновесия. На рис. 2.5, а пунктирными линиями схематично показаны зависимости сил притяжения и отталкивания, действующих на один атом, от расстояния между атомами в решетке. Сплошной линией представлена кривая, соответствующая результирующей силе. Эта кривая пересекает ось абсцисс в точке А, где отталкивающие и притягивающие силы уравновешиваются. Величина а0 соответствует равновесному расстоянию между атомами. [2]
Если препятствовать расширению кристалла при нагревании путем постепенного повышения давления, то аномальная теплоемкость оказывается выраженной менее резко. [3]
Ko: - iJnJniiuienT расширения кристаллов невелик, но выбирая в узком интервале возможных плотностей какую-нибудь из осуществимых плотностей кристаллов А, мы тем самым задаем температуру и, следовательно, плотность кристаллов В. Выше уже было отмечено, что изменения плотностей или, соответственно концентраций не могут быть отражены на рассматриваемых плоских диаграммах. [4]
В результате облучения происходит анизотропное расширение кристалла, аморфизацвя его структуры, уменьшение плотности, упругости, теплопроводности и др. Окислы меняют свойства аналогично силикатам, но в меньшей степени. [5]
Расширение графита при образовании его окиси напоминает расширение кристалла при образовании других слоистых соединений. [6]
Поэтому при последующем нагревании динаса лишь только часть расширения кристаллов и зерен может компенсироваться этими микротрещинами, так как каждый кристалл и каждое зерно не могут точно заполнить объем трещины. [7]
На рис. 4.41 схематически показано изменение полос роста по мере расширения кристалла. В начальный период роста направление полос параллельно поверхности ра стущего кристалла, но по мере его расширения полосы принимают изогнутую форму и вдоль них возникают боль шие напряжения. Эти границы являются местом зарождения дислокаций, имеющих вид радиально вытянутых прямых линий. Предполагают, что существует два механизма возникновения радиальных дислокаций на бороздах расширения. Один из них связан с локальными напряжениями, вызванными решеточным рассогласованием, которое возникает при большом температурном градиенте на границе раздела фаз. Другой обусловлен термическими напряжениями, образующимися при охлаждении в тепловом поле с радиальным температурным градиентом. Однако остается неясным, какой из двух механизмов преобладает в продессе генерации дислокаций. [8]
Коэффициенты теплового расширения по трем осям этого эллипсоида называются главными коэффициентами расширения кристалла. [9]
Тт) этот путь может представлять собой всестороннее сжатие расплава или же расширение кристалла. В го же время второй путь представляется менее надежным, принимая во внимание анизотропию аир для полимерных кристаллов ( см. гл. [10]
На регулировочных полосах роста при резких изменениях температуры, например в процессе расширения кристалла, изменения основного состава могут быть значительными. [11]
 |
Кристаллические ре-шетки. [12] |
С повышением температуры металла ( сплава) амплитуда колебаний увеличивается, что вызывает расширение кристаллов, а при температуре плавления колебания частиц усиливаются настолько, что происходит разрушение кристаллической решетки и металл плавится. [13]
Вспомним, что кристаллы обладают анизотропией, поэтому, вообще говоря, величина расширения кристалла при нагревании зависит от направления. Однако большинство твердых веществ имеет поликристаллическое строение, и потому они являются изотропными. Все изложенное дальше в этой главе относится к изотропным телам. [14]
Как только Фейнман начал размышлять о том, как изменяются межатомные силы по мере расширения кристалла, он тут же задумался о том, как поведут себя эти силы при сжатии кристалла, когда атомы приблизятся друг к другу. Он понял, что силы, действующие между парами атомов ( не только в кристаллах, но и в молекулах), можно рассматривать как маленькие пружинки. Любая пружина сопротивляется как растяжению, так и сжатию. Некоторая часть этой работы повторяла то, что уже сделали другие, но Фейнман этого не знал и разработал всю теорию сам, исходя из азов, что уже вошло у него в привычку. Подход Фейнмана основывался на том, что силу, действующую на любое ядро в молекуле или в кристаллической решетке, можно найти из распределения электрического заряда на соседних ядрах и в электронных облаках, окружающих эти ядра, согласно законам классической электростатики, если известно распределение электронного облака. Вам также понадобится и квантовая механика, чтобы найти распределение электрического заряда в облаке, но, как только вы это сделали, все остальное, собственно говоря, проще пареной репы. [15]
Страницы: 1 2 3