Значение - искомый параметр
Cтраница 1
Значение искомого параметра, вычисленное на основе ограниченного числа опытов, всегда будет содержать элемент случайности. Такое приближенное значение называется оценкой параметра. [1]
Для определения значения искомого параметра со по заданным значениям параметров е и в могут быть использованы таблицы приложения 4 в случае дрямо-тока и приложения 5 в случае противотока. Так как подобные таблицы могут быть составлены для любых взаимных направлений греющей и нагреваемой сред, то тем самым любая задача конструктивного расчета теплообменников может быть решена с помощью безразмерных параметров без определения средней разности температур А Ср, что существенно упрощает расчет. [2]
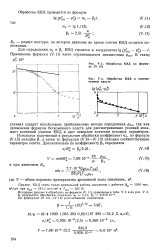 |
Обработка КВД по ле.| Обработка КВД в ограниченном пласте. [3] |
КВД и дает неверные значения искомых параметров. Используя полученный в результате обработки коэффициент alt по формуле (V.12) находим Р, а затем по формулам (V.4) - (V.10) находим соответствующие параметры пласта. [4]
В процессе поиска значения искомых параметров, которые приводят к нарушению указанных ограничений, следует отбрасывать. [5]
При этом методе значения искомых параметров дискретного регулятора постепенно увеличивают от малых начальных значений до тех пор, пока процесс в замкнутой системе не станет колебательным. После этого значения параметров регулятора уменьшают примерно наполовину. [6]
Величины а или а следует выбирать в качестве значений искомых параметров. [7]
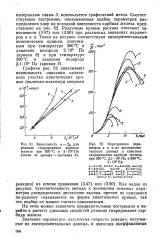
Как видно из рисунка, чувствительность метода к значениям искомых параметров распределения достаточно высока, причем их изменения по-разному сказываются на форме кинетических кривых, так что подбор их можно считать однозначным. [9]
 |
Структурно-функциональная схема метрологического звена. [10] |
Когда все перечисленные операции проделаны, на момент измерения становится известным значение искомого параметра и погрешность его измерения. [11]
 |
Схема жидкостного амортизатора с демпфированием энергии при ходе распрямления. [12] |
Ввиду сложности процесса демпфирования расчет производят, принимая ряд допущений и осредняя значения искомых параметров. [13]
Теперь мы можем рассчитать любой из размеров обрамляющего бокса или параметры кернинга для заданного варианта шрифта, используя значения искомых параметров в восьми ( или четырех в случае Myriad) основных файлах и вычисляя их интерполированное значение. [14]
Если одной из независимых переменных в рассматриваемой задаче является время t, то задаются некоторые условия ( например, значения искомых параметров) в на-ч-альный момент t0, называемые начальными условиями. Задача, которая состоит в решении уравнения при заданных начальных условиях, называется задачей Коши для уравнения с частными производными. При этом задача решается в неограниченном пространстве и граничные условия не задаются. Задачи, при формулировке которых ставятся граничные и начальные условия, называются нестационарными ( или смешанными) краевыми задачами. Получающиеся при этом решения меняются с течением времени. [15]
Страницы: 1 2 3 4