Ребро - параллелепипед
Cтраница 1
Ребра параллелепипеда имеют длииы 2, G, 9, Найти проекции этих ребер на направление диагонали. [1]
Ребра параллелепипеда, равные а и Ь, взаимно перпендикулярны, а ребро, длина которого равна с, образует с каждым из первых двух ребер угол а. [2]
Ребра параллелепипеда, выходящие из этой вершины, лежат на ребрах тетраэдра. Грани ABC тетраэдра может принадлежать лишь вершина параллелепипеда, не лежащая с вершиной D в одной грани. Такая вершина только одна, ее обозначим FI. [3]
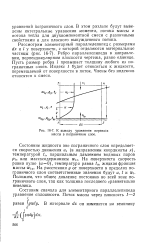 |
К выводу уравнения переноса массы в пограничном слое. [4] |
Ребро параллелепипеда в направлении, перпендикулярном плоскости чертежа, равно единице. Пусть размер ребра / превышает толщину любого из по-граничньпх слоев. [5]
Ребра параллелепипеда, выходящие из этой вершины, лежат на ребрах тетраэдра. Грани ABC тетраэдра может принадлежать лишь вершина параллелепипеда, не лежащая с вершиной D в одной грани. Такая вершина только одна, ее обозначим FJ. [6]
Ребра параллелепипеда, определяющие элементарную ячейку, должны быть параллельны соответствующим кристаллографическим осям. Таким образом, представление о параллелепипедах, использованное ранее для выражения симметрии кристаллов, может быть принято и для элементарных ячеек. [7]
Ребра параллелепипеда описываются векторами х 2у, 4у и у 3z, идущими из начала координат. [8]
Ребра параллелепипеда, выходящие из, этой вершины, лежат на ребрах тетраэдра. Грани ABC тетраэдра может принадлежать лишь вершина параллелепипеда, не лежащая с вершиной D в одной грани. Такая вершина только одна, ее обозначим FI. [9]
Каждое ребро параллелепипеда равно а. [10]
Длины ребер параллелепипеда равны а, Ь и с. [11]
Длины ребер параллелепипеда равны a, b и с. [12]
Длины ребер параллелепипеда равны а, Ь и с. [13]
Длины ребер параллелепипеда равны a, b и с. [14]
Длины ребер параллелепипеда равны а, Ь я с. [15]
Страницы: 1 2 3 4