Ребро - параллелепипед
Cтраница 2
Длины ребер параллелепипеда равны а, Ь и с. [16]
Длина ребер параллелепипеда вдоль осей X, Y, Z равна соответственно а, Ь, с. [17]
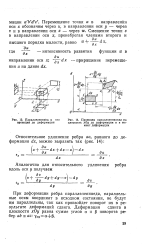 |
Параллелепипед и его проекции до деформации.| Проекция параллелепипеда на плоскость хОу до деформации и в момент деформации. [18] |
При деформации ребра параллелепипеда, параллельные осям координат в исходном состоянии, не будут им параллельны, так как произойдет поворот их в результате деформаций сдвига. [19]
Обозначим длины ребер параллелепипеда X, Y, Z; введем при решении задачи декартовы координаты, начало которых О поместим в центре параллелепипеда. [20]
Через концы трех ребер параллелепипеда, выходящих из одной вершины, проведена плоскость. Опрелелить, в каком отношении она делит диагональ параллелепипеда, выходящую из той же вершины. [21]
Через концы трех ребер параллелепипеда, выходящих из одной вершины, проведена плоскость. Определить, в каком отношении она делит диагональ параллелепипеда, выходящую из той же вершины. [22]
Сумма длин всех ребер параллелепипеда должна быть равна 20 см. При каких размерах коробки площадь ее поверхности будет наибольшей. [23]
Сумма длин всех ребер параллелепипеда должна равняться 20 см. При каких размерах коробки ее полная поверхность будет наибольшей. [24]
Через концы трех ребер параллелепипеда, выходящих из одной вершины, проведена плоскость. [25]
 |
Определение угловых деформаций частицы жидкости. [26] |
За счет удлинения ребер параллелепипеда происходит изменение его объема. [27]
Середины трех попарно скрещивающихся ребер произвольного параллелепипеда соединены. Докажите, что точка пересечения медиан полученного треугольника совпадает с центром параллелепипеда. [28]
Аналогично выражаются два других ребра параллелепипеда. [29]
Стержень скользит по ребру параллелепипеда без трения. [30]
Страницы: 1 2 3 4