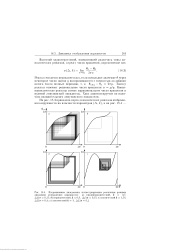
Квазипериодический режим

Cтраница 1

Итерационные диаграммы, иллюстрирующие различные режимы динамики отображения окружности. а квазипериодический, k 0 7, Д / 2тг 0 35. б периодический, k 0 9, Д / 2тг 0 35. в хаотический k 1 56, Д / 2тг 0 4. г хаотический k 3, Д / 2тг 0 2. [1]

Квазипериодические режимы имеют иррациональное число вращения и нулевой ляпуновский показатель. Хаос диагностируется по наличию положительного ляпуновского показателя. [2]

Статистически равновесный квазипериодический режим в системе АОС был достигнут приблизительно за год. [3]

Статистически равновесный квазипериодический режим в системе ДОС был достигнут приблизительно за год. [4]

Переход через перемежаемость к квазипериодическому режиму у края языка Арнольда в отображении Заславского ifn i fn A ksa ( fn dpn, Pn i dpn ksiinpn при d 0 3, fc 0 5, Д / 2тг 0 1136 ( a, 0 1137 ( 6, 0 1138 ( в. [5]

Фактически это квазипериодический режим. Механизм реинжекции в данном случае очень простой, он связан с периодичностью пространства состояний по фазовой координате. Причина отсутствия хаоса состоит в том, что при выбранном значении параметра k 0 5 динамика на стадиях переключения не обладает высокой чувствительностью по отношению к возмущениям начальных условий. [6]

С топологической точки зрения квазипериодические режимы неустойчивы, а синхронные устойчивы: при фиксированном е и изменении г синхронные режимы наблюдаются на интервалах ту, а квазипериодические - в отдельных точках. Это означает, что квазипериодическое движение можно разрушить сколь угодно малым возмущением. Однако с вероятностной точки зрения квазипериодические режимы преобладают 11 поскольку, как было доказано Арнольдом [1961], при малых е мера Лебега всех интервалов синхронизации стремится к нулю при е - 0; это означает, что возмущения, разрушающие квазипериодичность, довольно маловероятны. [7]

Фаза как частица в наклонном потенциале V ( VO - ( a Слу-чай синхронизации. частица сидит в минимумах потенциала. ( Ь Вне области синхронизации частица скатывается вниз. Из [ Pikovsky et al. 2000 ]. [8]

Шум слабо влияет на квазипериодический режим: здесь средняя скорость частицы не равна нулю, и она слабо меняется в присутствии шума. Влияние же шума на синхронное состояние может быть весьма сильным. Действительно, шум может выбить частицу из устойчивого состояния; если он достаточно велик, то он может перевести частицу в соседнее устойчивое положение. При этом фаза меняется на 2тг, это явление называют проскоком фазы ( phase slip), оно показано на рис. 9.2. Чтобы произошел проскок, частица должна преодолеть потенциальный барьер AV, так что вероятность проскока может быть мала. В общем случае вероятность проскока растет с интенсивностью шума и убывает с высотой барьера, поэтому, если v ф 0, то вероятности проскоков 2тг и - 2тг различны, и частица в среднем движется в одну сторону. Наблюдаемая при этом разность частот Ci ( чр) не равна нулю. Изменение фазы во времени напоминает случай чисто детерминированной системы вблизи порога синхронизации ( ср. [9]

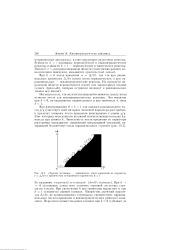Чертова лестница - зависимость числа вращения от параметра г А / 2тг в критическом отображении окружности, k 1. [10]

В области k 1 возможны периодические и квазипериодические режимы, в области k 1 - периодические и хаотические режимы. Линия k 1, разграничивающая области существенно разного динамического поведения, называется критической линией. [11]

При увеличении С наблюдались как резонансы различных порядков, так и переходы от квазипериодических режимов к хаотическим. [12]

Если количество неустойчивостейг каждая из которых приводит к дополнительной модуляции, достаточно велико, многочастотный квазипериодический режим выглядит чрезвычайно сложным. [13]

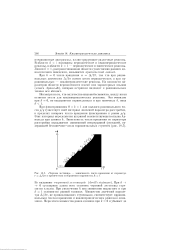Чертова лестница - зависимость числа вращения от параметра г А / 2тг в критическом отображении окружности, k 1. [14]

Несмотря на то, что количество языков бесконечно, между ними остается место для квазипериодических режимов. [15]

Страницы: 1 2 3